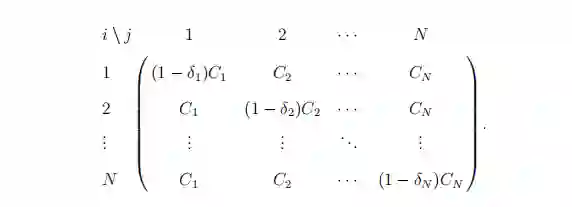【博士论文】《博弈论在安全领域的应用》罗格斯新泽西州立大学208页论文

学位论文摘要

在这篇论文中，我们研究了博弈论在确定各种基础设施保护策略的应用。博弈模型是在防御者和对手之间进行的。防御者寻求最小化对基础设施网络的损害，而对手的目标则是最大化。本论文分为两部分。在第一部分，我们考虑资源分配博弈模型，在第二部分，我们研究巡逻和搜索博弈。

在资源分配博弈领域，我们解决了文献中现有的一些限制。其中一个限制是，这些模型大多假设博弈的参数是确定的，或者遵循一个已知的分布。而在现实中，博弈的某些参数可能是不确定的，没有已知的分布，或者关于它们的分布信息可能是不可靠的。为此，我们研究了目标估值不确定情况下的一次性安全博弈。我们提出了一个模型，在这个模型中，双方都使用一种稳健的方法来应对目标估值的不确定性。我们表明这个模型的纳什均衡是门槛型的，并开发了封闭式的解决方案来描述均衡点的特征。然后，我们将我们的模型应用于向美国10个城市地区分配安全资金的真实案例。

另一个限制是缺乏解决分层决策的模型。保护基础设施及其用户免受蓄意攻击，需要在组织结构中做出战略和运行决策。尽管通常是分开分析的，但这些决策是相互影响的。为了解决这个问题，我们开发了一个两阶段的博弈模型。在第一阶段，玩家做出投资决策，在第二阶段，他们决定保卫/攻击哪些网站。我们区分了在第二阶段出现的两种类型的博弈。最大损害博弈和渗透/骚扰博弈。我们证明，在预算约束下，这个博弈的解决方案是唯一的。事实上，当第二阶段的博弈是渗透/骚扰类型时，投资-防御博弈有一个独特的闭式解，这是非常直观的。结果显示，增加对一个目标地点的防御投资会降低防御和攻击该目标的概率。然而，攻击投资的增加会增加防守和攻击该目标的概率。同样，防御者（攻击者）投资效率的提高会导致防御者和攻击者的投资减少（增加）。我们还将提出的模型应用于一个真实的案例。真实数据的结果表明，攻击者从失败的攻击中得到的惩罚是决定防御者的投资和防御概率的最佳分布的重要因素。防御者的第二阶段防御决策是对第一阶段投资决策的补充。也就是说，在得到很少或零投资的目标地点中，最重要的一个地点在第二阶段以相对高的防御概率被覆盖。此外，随着攻击者预算的增加，防御投资从不太重要的站点转移到更重要的站点。

我们还研究了资源分配模型中的总体性保护选项。总体保护指的是同时保护多个目标的选项，例如，应急响应、边境安全和情报。大多数带有总体保护的防御性资源分配模型都假定只有一个总体保护选项可以保护所有目标。然而，这可能并不现实，例如，应急反应投资可能只覆盖某个区域。为了解决这个问题，我们开发了一个新的资源分配模型，以适应针对故意攻击的通用总体保护。该模型还考虑了多种自然灾害类型。我们表明，我们提出的模型是一个凸优化问题，因此可以在多项式时间内求解到最佳状态。此外，整个国家层面的资源分配问题可以被分解成更小的城市层面的子问题，从而产生一个更有效的算法。数字实验证明了所提方法的性能。

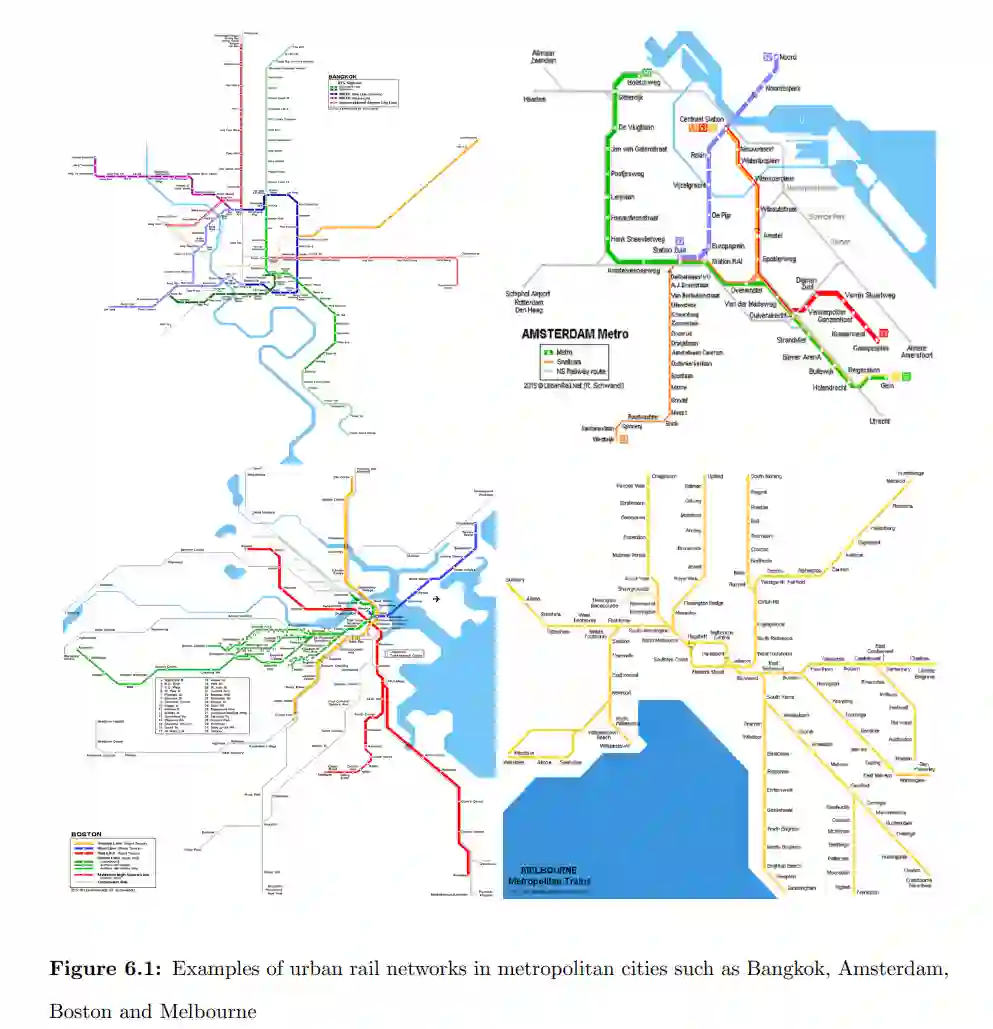
巡逻和搜索博弈通常是在一个图上进行的，玩家在一个时间范围内做出决策。在巡逻博弈中，防御者控制一组巡逻者并指挥他们在图上行走，以尽量减少对手的攻击损失，而对手则选择一个目标和攻击时间。为了成功地摧毁一个目标地点，对手需要一些准备时间而不被巡逻者打断。大多数巡逻博弈模型都假设站点的价值是相同的，或者说它们不会随时间变化。然而，这并不是一个现实的假设。特别是在软目标的情况下，这些值可能对应于一个地点的占用水平，因此，这样的值可能是不同的，并可能随时间变化。我们提出了具有随时间变化的节点值和基于节点的攻击时间的新模型。我们使用列生成、列和行生成等算法数值地解决这些模型。我们将这些算法应用于美国一个主要城市的城市铁路网的真实案例。结果显示了所提出的解决方法的效率。他们还证明了额外的巡逻员的回报率是递减的。

在搜索博弈中，一个隐藏者将一组物体隐藏在一组潜在的隐藏地点。搜索者控制一组搜索队，指挥他们在网络上行走，找到隐藏的物体，使目标函数得到优化。然而，在某些情况下，玩家可能会将藏匿地点相互区分开来，目标是优化加权搜索时间。为了解决这个问题，我们引入了一个新的离散搜索博弈，并考虑到了不同地点的权重。我们表明，在某些条件下，该博弈有一个封闭式的纳什均衡。对于一般情况，我们开发了一种基于列和行生成的算法。我们表明搜索者的子问题是NP-hard的，并提出了一个分支和价格算法来解决它。我们还提出了一个用于Hider子问题的多项式时间算法。数值实验研究了该方法的性能，并揭示了对该博弈特性的洞察力。

第一章 简介

恐怖袭击是对国民经济和生活质量的一个严重关切。每年都有成千上万的人因为这些袭击而丧生或受伤或被绑架。2015年，全世界共发生11774起恐怖袭击事件，造成28300多人死亡，35300多人受伤。此外，有超过12,100人被绑架或劫持为人质[22]。恐怖主义的持续威胁带来的心理影响也是相当大的。这类事件在社会上造成了恐惧、惊慌、焦虑和苦恼。

保护关键基础设施不受恐怖主义侵害是国土安全的首要任务之一[104]。对关键基础设施的物理保护可以防止成功实施高影响力的恐怖袭击。此外，对针对关键基础设施的恐怖袭击作出即时反应，可以防止与此类袭击相关的连带效应。

这些原因以及在过去几十年中发生的许多引人注目的恐怖袭击，突出了此类基础设施的安全建模和分析是一个主要的研究议程。通过评估与基础设施内每个站点相关的风险、缓解计划以及设计保护战略和响应政策，可以大大减少攻击的后果。基础设施安全最近成为研究人员越来越感兴趣的主题。人们提出了不同的方法来模拟安全问题中的战略互动，这些方法包括系统分析[115]、数学建模[51]、概率风险分析[33, 39, 73, 100, 115, 116]，以及对抗性风险分析[123]。然而，由于恐怖分子的攻击可能是战略性的，对这种攻击的博弈论分析会产生更真实的结果。因此，最近的研究集中在开发博弈论模型来捕捉恐怖主义风险，并将结果应用于加强安全措施。其中一个模型ARMOR[112, 113, 114, 118]已被部署在洛杉矶国际机场（LAX）以加强机场的安全。

这项研究的重点是博弈论的应用，为各种基础设施寻找最佳保护策略，以抵御蓄意攻击。这项工作可以分为两部分：资源分配模型，以及巡逻和搜索博弈模型。

为防止蓄意攻击而进行的资源分配通常是昂贵的，决定如何分配资源以保护关键基础设施是一个困难的问题。许多因素会影响这种分配政策，例如，在实践中，公平在确定防御分配方面起着重要作用[129]。此外，创造一种平衡以保护不同类型的威胁（例如，生物攻击与炸弹攻击，或恐怖主义与非恐怖主义预防活动之间）是另一个因素。其中一些因素已经在静态安全博弈的文献中得到了解决。然而，仍然有一些限制。例如，大多数基础设施安全博弈假设博弈的参数是确定的或遵循一个已知的分布。而在现实中，博弈的一些参数可能是不确定的，没有已知的分布，或者关于它们的分布信息可能是不可靠的。在这项研究中，我们建立了具有和不具有私人信息的不完全信息基础设施安全博弈的稳健无分布模型。此外，决策的层次性在文献中经常被忽略。然而，分配资源以保护关键的基础设施涉及到组织结构中不同层次的决策：战略和运行决策。这些决策相互影响，需要同时进行研究。在这项研究中，我们开发了两阶段的博弈模型来解决这个问题。此外，大多数现有的带有总体保护选项的资源分配模型都假定只有一个总体保护选项可以保护所有目标。然而，在现实中，可能有许多总体保护方案，而每个方案可能只覆盖一个子集的目标。为了解决这个问题，我们开发了一个新的资源分配模型，该模型具有通用的总体保护选项。我们还开发了高效的分解算法来寻找最佳的资源分配。

巡逻和搜索博弈通常是在一个图形上进行的，玩家在一个时间范围内做出决定。设计巡逻队来保护开放的大众运输系统和其他软目标带来了独特的挑战，这些挑战在巡逻博弈的文献中还没有被解决。其中一个挑战是这些系统内人群规模的动态性质。因为对手的主要目标是造成人员伤亡，所以节点的价值取决于居住在这些节点的人数。这些数字随着时间的推移而变化，恐怖分子往往根据这些变化来确定他们的攻击时间[68]。其他挑战包括处理多个攻击者，适应人力资源的限制，以及开发有效的方法来设计一般网络的巡逻。我们通过开发具有动态变化的节点值、基于节点的攻击时间、多个巡逻员和多个攻击者的新模型来应对这些挑战。为了有效地解决这些模型，我们开发了先进的解决算法，如列生成，以及列和行生成。在搜索博弈中，一个隐藏者将一组物体隐藏在一组潜在的隐藏地点。搜索者控制一组搜索队，指挥他们在网络上行走，找到隐藏的物体，从而使目标函数得到优化。大多数搜索博弈模型都假定隐藏地点是相同的，玩家的目标是优化搜索时间。然而，在某些情况下，玩家可能会将藏匿地点相互区分开来，目标是优化加权搜索时间。为了解决这个问题，我们引入了一个新的离散搜索博弈，并考虑到了不同地点的权重。

1.1 问题陈述和研究动机

本研究考虑的主要问题是确定针对故意破坏（如恐怖袭击）的最佳保护策略。因为对手的决策也是有策略的，所以对这些问题的博弈论分析会产生更现实的结果。本研究中考虑的博弈模型是在防御者（她）和对手（他）之间进行的。防御者想要最小化对基础设施网络的损害，而对手则想要最大化。这些模型可以分为两类：资源分配博弈，以及巡逻和搜索博弈。在资源分配模型中，有一个N个目标的集合。每个目标i都有一个Ci的值。防守方决定防守哪个目标，而对抗方决定攻击哪个目标。如果双方都选择相同的目标i，那么以δi的概率，攻击将被检测并挫败。这个概率被称为检测概率。以下矩阵的(i, j)部分显示了如果防御者选择目标i，而对手选择目标j的预期损害。注意，这个矩阵对应于对手的报酬矩阵，对手试图使预期损害最大化。

我们的目标是在各种条件下，如博弈参数的不确定性和私人信息的存在，以闭合形式描述纳什均衡（NE）的特征。

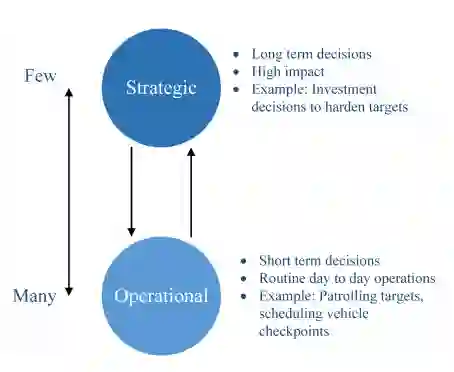
我们在这篇论文中讨论的另一个问题是决策的层次性。保护基础设施及其用户不受破坏，需要在一个组织的层次结构中做出战略和运行决策（见图1.1）。战略决策是具有长期影响的长期决策。例如，对目标站点进行 "加固"[17]以减少攻击的成功概率的投资决策被归类为战略决策。这包括对新技术的投资，以加强网站的安全性。另一方面，运行决策是与日常运作有关的短期决策，如巡逻、分配第一反应者和安排车辆检查站。请注意，"战略 "这个词也可以用来描述参与者。在这种情况下，"战略玩家 "指的是一个理性的玩家，其目标是最大化回报。因此，在本论文中，"战略决策 "是指具有长期影响的长期决策，"战略参与者 "是指以报酬最大化为目标的理性参与者。大多数研究只关注纯粹的战略决策[63, 107]或纯粹的运行决策[16, 35, 36, 38]。然而，这些决策是相互影响的。例如，在某一区域安装闭路电视摄像机可能会使该区域的巡逻变得不必要。或者将金属探测器和安检系统分配给目标地点，可能会影响到这些目标中巡逻队的最佳调度。此外，投资一项新技术以加强某个目标地点的安全，可能会降低其目标的吸引力，影响保卫该目标的最佳概率。因此，在同一个模型中考虑战略和行动决策会产生一个更全面的分析。

图1.1: 战略决策与运行决策

我们研究了在考虑到人为和自然灾害的资源分配模型中总体保护方案的影响。总体保护方案是指可以同时保护多个目标的替代方案。例如，对边境安全和情报工作的投资有望保护多个目标免受恐怖主义的威胁。这一领域现有文献的局限性在于，大多数现有的模型只考虑了保护所有目标的单一总体性保护方案。然而，这可能不是对现实的准确表述。例如，对边境安全的投资可以分为不同的入境点，每一个入境点预计都会使离该特定入境点较近的地区受益。为此，一个新的资源分配模型，容纳多个保护目标子集的总体保护措施，将导致一个更现实的分析。

本研究中调查的巡逻博弈G是一个由防御者和对手在连接图Q = (N , E)上进行的零和博弈，节点集为N，边集为E，时间跨度为T。防御者控制着一组安全人员（巡逻者）S，并指示他们在图上行走，以尽量减少来自对手的攻击的损害。而敌方控制着一组攻击者A，并为每个攻击者选择一个节点和一个攻击时间。为了成功地摧毁一个目标站点，攻击者需要在目标上有一定数量的时间单位，不被任何巡逻者打断。巡逻博弈文献中的大多数论文都假设对手选择一个目标进行攻击，目标值在一段时间内是固定的，有些甚至假设所有目标是不可区分的，即它们都有相同的价值。然而，在许多现实情况下，情况并非如此。例如，在一个交通设施中，每个地点的人数、占用水平可以被认为是该地点的价值。此外，占用水平可能随时间变化，预计在高峰期，占用水平会比正常时间高。因此，一个具有随时间变化的节点价值、特定节点的攻击时间、多个巡逻者和多个攻击者的巡逻博弈模型将导致与现实更加一致的结果。

本研究中考虑的搜索博弈是在搜索者和隐藏者之间进行的。搜索者控制一组S个搜索队，隐藏者控制一组H个要隐藏的对象。博弈是在一个完整的图Q = (N , E)上进行的，其中N = {0, 1, 2, . ，N}是图中节点的集合，E = {(i, j) : i, j∈N, i 6 = j}是边的集合。文献中的大多数搜索博弈模型都假设藏身之处是相同的，玩家的目标是优化搜索时间。然而，在某些情况下，玩家可能会将藏身之处相互区分开来，其目标是优化加权搜索时间。例如，在某些攻击中（生物或化学），伤亡率取决于人口密度、环境条件等因素。因此，不同的地点可能有不同的伤亡率，而整体的损失将与暴露时间和伤亡率成正比。另一个例子是通过通信渠道检测窃听者的问题[37]。不同的信道可能有不同的传输能力，对网络的破坏率将与检测时间和信道的容量成正比。此外，藏匿地点可能分散在大片区域，搜索可能涉及多个搜索小组。为此，一个新的搜索博弈，容纳了不同地点的不同权重，将导致一个更现实的分析。

1.2 研究贡献

在这项研究中，提出了新的博弈论模型，以解决资源分配博弈、巡逻和搜索博弈领域中的一些现有差距。在资源分配博弈领域，主要贡献是：扩展现有模型以处理分层决策；引入广义的总体保护方案；用稳健的方法解决参数的不确定性；开发适合于更有效算法的新模型。在巡逻和搜索博弈领域，我们的主要贡献是：纳入了与时间相关的节点值，以及多个巡逻者和多个攻击点；并引入新的和更有效的算法来解决博弈论模型。

在接下来的章节中，我们将介绍我们的主要贡献，如下所述。

1.我们开发了一种稳健的方法来应对安全博弈中的参数不确定性，并在第二章提供了闭合形式的NE策略。

2.为了解决防范蓄意攻击的决策的层次性问题，在第三章中，我们引入了一个两阶段的投资-防御博弈模型，并推导出某些条件下的闭合形式的NE策略。这个模型抓住了战略投资决策和运行攻击/防御决策的综合效应。

3.在第四章中，我们提出了一个新的资源分配模型，用于保护资产免受人为和自然灾害的影响，并具有广义的总体保护。这个模型被证明导致了一个可分解的凸优化问题，因此可以被有效解决。

4.在第五章和第六章中，我们介绍了新的巡逻博弈模型，该模型具有与时间相关的节点值，基于节点的攻击时间，多个巡逻者和多个攻击点；并开发了高效的解决方法，基于列生成，以及列和行生成来解决现实的大小问题。

5.我们在第七章中介绍了一个新的搜索博弈模型，该模型具有不同的节点权重、多个搜索队、多个隐藏对象和分散的隐藏地点；并在第七章中介绍了基于列和行生成的高效求解方法，以解决现实的大小模型。

6.我们在第八章中提出了本研究的结论并讨论了未来的研究思路