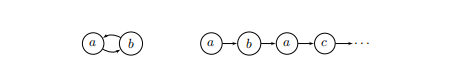为了实践知识表示，知识表示语言具有形式化的语义是最重要的。然而，由于有许多不同的语言都具有形式化的特点，因此有一个统一的框架来捕捉语言和逻辑的语义是很有价值的。一个这样的框架就是理由论，在这个框架中，语义是通过使用解释来定义的，在我们的术语中称为理由。直观地说，一个理由是一个解释某些事实的真值的图。然而这引入了一个潜在的问题：一个事实的理由状态和它的否定可能是不一致的。因此，为了使辩解语义得到良好的定义，这些状态应该是相反的。这样的语义学被称为是一致的。

在本论文的第一部分，我们证明了理由论的主要语义实际上是一致的。此外，我们还证明了对理由的有用结果，比如将理由组合在一起的能力。理由论语义学的另一个问题是，有不同类别的理由，这可能导致不同的语义学。我们表明，这两个看似不相关的问题实际上是有深刻联系的。

之后，我们在理由论和博弈论之间建立了一种联系，这使得理由可以被看作是双人博弈中的策略。这种联系通过在系统是有限的情况下为语义提供一个一般条件，为正当性理由论中的这两个问题提供了一个解决方案。

理由论并不是非单调逻辑语义学的唯一统一框架。另一个著名的框架是近似定点理论（approximation fixpoint theory），它在本质上更加代数化。我们在证明理由论和近似定点理论之间建立了一种联系。近似定点理论的终极语义的概念可以转移到理由语义的领域。这使得证明语义学可以比以前捕获更多的语义。

作为本论文的最后一个主题，我们研究了理由的嵌套，它可以用来定义模块化语义。在以前的嵌套定义中，由于使用了压缩操作，大量的信息被丢失。我们提供了一个替代的、更普遍的定义，没有这个缺点。这允许基于理由的更直观的模块化语义。我们证明，这与树状理由的压缩是等价的，在特殊情况下，对于图状理由也是如此。我们也研究了这两种方法的一致性，作为额外的奖励，我们解决了树状证明的一致性问题。

综上所述，本论文收集了证明理由论中的一些进展，并以实例说明了这些进展。

第1章绪论

1.1 背景

本论文位于人工智能（AI）领域，特别是知识表示和推理（KRR）子领域。KRR的主要关注点是定义表示知识的语言和逻辑，并构思用这些知识进行推理的工具和技术。当然，这是一个过于简化的观点，但它使我们能够看到更大的画面。要想拥有一个完美的推理器，首先应该捕捉问题领域的知识，然后释放出手头的推理能力。我们应该将其与人工智能其他部分的函数拟合方法进行对比，比如深度学习。这些方法虽然对其他问题（如语音识别）非常有用，但由于其近似的性质，并不总是能够推理出100%的逻辑正确。Darwiche（2018）将人工智能的这种二分法定义为基于模型与基于函数的人工智能。基于模型的人工智能与基于函数的技术相比有一个明显的优势：内部机制通常也被捕获，与基于函数的技术相比，它们的行为就像黑盒。因此，相对于更不透明的基于函数的方法，这些方法更倾向于可解释的系统。此外，基于函数的人工智能通常是为一个特定的目标量身定做的。基于模型的人工智能的一个主要部分是知识表示和推理（KRR）。代表性的知识可以用来解决多个问题；因此它是面向多目标的。这个想法是知识库范式的核心（Cat等人，2014；Denecker和Vennekens，2008）。因此，这些技术可以更好地处理新的场景，例如在因果推理中。由于人工智能的法规和政策，例如解释权，基于模型的方法的更高程度的可解释性显得越来越重要。拥抱解释将是实践当代知识表示和推理（KRR）的一个完美起点。

在KRR中，许多语言和逻辑被发明用于不同的目的，从语义网本体语言（Antoniou和van Harmelen，2009；Baader等人，2005）到机器人学（Paulius和Sun，2019），立法和法律（Jones，1990）。通常情况下，这些逻辑都是基于相同的原则，但在工作中略有不同，或者是从不同的角度来解决。为了看清大局，最重要的是我们能在不同的语言和逻辑之间建立关系：它们是具有相同基本原则的不同方言，还是有本质的不同。研究这些关系的一种技术是定义语言之间的转换。特别是，我们可以找到一种语言对另一种语言的嵌入。然而，由于现有的知识表示语言数量庞大，这是不现实的。另一个更可行的方法是设想统一一大批逻辑学的语义的框架。

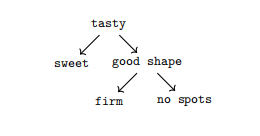
幸运的是，证明理论既解决了可解释性的问题，也解决了统一性的问题。理由论的语义（意义）是基于理由的概念，它是一个解释某事为何成立的图3。例如，理由（在这一点上完全理解这些图片并不重要）作为一种解释，为什么一个苹果是美味的（当然你对美味的定义可以不同）。

理由语义学的工作方式是给每个理由打分，说明它是否好。通过改变我们对理由的评级方式，我们可以改变同一领域的语义。为了改变领域，辩解理论使用一套规则作为构建解释的基础。因此，不难看出，辩解理论作为一个统一的框架。再加上理由（解释）是语义的主要构成部分，理由理论是KRR的一个很好的研究对象。

1.2 KRR中的理由说明

本论文所详述的理由理论起源于Denecker（1993）的博士论文，并由Denecker, Brewka, and Strass（2015）进一步正式化。理由--尽管并不总是以Denecker（1993）；Denecker等人（2015）所描述的确切形式出现--以不同的方式出现在KRR的不同领域中。理由论起源于逻辑编程，其中理由的概念已经存在了相当长的时间。根据Fandinno和Schulz（2019）的说法，理由的概念起源于Shapiro（1983）；Sterling和Lalee（1986）关于调试的工作。在这项工作的基础上，Lloyd（1987）为声明式错误诊断器引入了不正确的规则和未发现的原子的概念。这些概念说明了什么时候一个结构不是给定逻辑程序的模型。第二年，Sterling和Yalçinalp（1989）用元解释器解释了Prolog专家系统。1990年，Fages(1990)用理由来定义逻辑程序的稳定语义，在这种情况下，理由是原子的集合。很多论证方法都使用了支持集/值的概念，这个概念是由Pereira等人（1992，1993）首次提出的。这大约是在Denecker和Schreye（1993）介绍早期版本的论证理论的同一时间。2000年，Roychoudhury等人（2000）通过为逻辑程序提供理由来证明基于表的证明。

Fandinno和Schulz（2019）列举了除了证明理论之外的几种突出的答案集编程（ASP）的证明方法。

离线论证（Pontelli和Son，2006)
基于标签的假设论证的答案集（LABAS）论证（Schulz和Toni，2016）。
因果证明（Cabalar和Fandinno，2016；Cabalar等人，2014)
Why-not出处（Damásio等人，2013年）
基于规则的论证（Béatrix等人，2016)

前三种方法与论证理论相似，因为论证也是字词或规则之间的依赖图。

离线证明（Pontelli and Son, 2006）是一种图结构，描述了一个原子相对于给定答案集的真值。因为离线论证只使用原子作为节点，所以节点必须用 "+"或"-"来表示它是真的还是假的。同样地，边也必须用 "+"和"-"来表示正或负的关系。负数字的真实性被认为是真实的，不做进一步解释。

LABAS论证（Schulz和Toni，2016）与离线论证非常相似，但它们对中间的规则应用进行了抽象。所以他们只指出有问题的字词和推导中使用的规则中出现的事实。此外，否定字词的真实性不是假设的，而是根据基础原子的真值来进一步解释。

因果图论证（Cabalar and Fandinno, 2016, 2017; Cabalar et al., 2014），与离线和LABAS论证相反，被用来对因果知识进行形式化和推理，这是它的主要焦点。它们也可以用来解释为什么一个字词包含在一个答案集中。此外，还定义了一个用于组合论证的代数。

Why-not provenance（Damásio等人，2013）是基于数据库文献的。这里的论证不是基于图的，而是用来解释原子的真值。

基于规则的证明（Béatrix等人，2016）是在基于规则的答案集计算的背景下定义的（Lefèvre等人，2017）：搜索算法猜测的是规则的应用或不应用，而不是原子的真值。ASP-求解器ASPeRiX使用这些理由进行反跳。

对不同论证方法之间错综复杂的差异感兴趣的读者应该看看Fandinno和Schulz（2019）的出色工作。除了这些方法，还有一些应用也使用了论证方法。Mariën（2009）；Mariën等人（2005，2007，2008）关于归纳定义的工作将理由作为归纳定义的推理技术的语义基础。理由被用来进行非因果的局部搜索（Järvisalo等人，2008）。类似于理由的数据结构也被用于答案集求解器的实现中（它们构成了无根据集算法中所谓的源-指针方法的基础（Gebser等人，2009））。此外，理由被证明是分析懒人接地背景下冲突的关键（Bogaerts和Weinzierl，2018）。最近，Lapauw等人（2020）使用理由来改进奇偶性博弈求解器。

1.3 研究目的和动机

从广义上讲，我们的目标是推进论证理由论。特别是，在本文中，我们广泛地研究了两个带有相关研究问题的属性。

第一个属性是关于正当化语义的合理性。理由论的一个好处是它提供了很大的自由度，可以通过分支评价的方式来创建新的语义。这些评价为解释图中的路径赋值，从而决定一个理由是否被认为是好的。在论证理由论中，一个事实和它的否定之间没有真正的区别。这意味着一个事实和它的否定都可以有好的理由，这在正常情况下被认为是一种矛盾。例如，如果你有一个很好的理由说明x成立，又有一个很好的理由说明x不成立，那么我们就得到一个矛盾。如果这种矛盾没有发生，我们就说它的正当性语义是一致的。

理由论最初是为了捕捉归纳定义的语义而开发的。归纳定义在数学中极为重要，因为它们被用来生成数学对象，如子集生成的子群、博勒集、自然数、递归公式、逻辑中的真值关系等（Buchholz等人，1981）。引用甘迪（1974年，第265页）的话来说

数学逻辑当然渗透着归纳性的定义

例如，我们可以在给定父关系的情况下归纳定义祖先关系，规则如下：

如果一个人p是q的父母，他就是q的祖先。
如果有一个人r，使p是r的父母，并且r是q的祖先，那么p就是q的祖先。

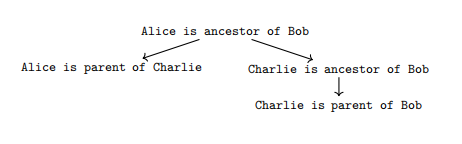
直观地讲，这应该是很清楚的意思。然而，一组归纳规则的形式语义并不立即清楚。一般来说，有两种方法可以为归纳定义提供形式语义。第一种方法是构造性的，从下往上建立关系：你从空的关系开始，反复地应用归纳定义中的规则，直到关系停止增加。第二种方法是将关系定义为满足归纳规则的最小的关系。如果归纳规则中不出现否定，这两种方法都能提供相同的结果，然而当涉及到否定时，这种方法就失效了。正当化理论遵循构造方法，但将其扩展到更广泛的构造类别。在这个意义上，我们可以把正当化看作是对一个事实为什么属于一个集合/关系的构造。回到祖先关系，下面的理由代表了为什么Alice是Bob的祖先的构造过程。

上面的论证描述了Alice是Bob的祖先的过程：需要哪些归纳规则。

仍然存在的问题是，像Bob不是Alice的祖先这样的事实的理由意味着什么。这样的理由提供了一个证据，说明为什么鲍勃是Alice的祖先是不可构造的。可建构性的概念当然是经典的：某物不可能既在一个关系中又不在一个关系中。这意味着，研究理由语义的一致性是最重要的。

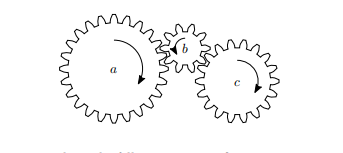
第二个属性更关心我们的解释可以是什么形状。用更专业的术语来说，理由是有向图。然而，我们允许两种形式，一种是总是做出相同的 "选择"，另一种是可以做出多种选择。让我们看一下一个联锁齿轮的例子。

在这种情况下，我们有以下两个理由：

在左边，你看到一个循环推理，第一个齿轮的顺时针转动被第二个齿轮的逆时针转动所证明，反之亦然。而在右边，第一个齿轮的顺时针转动首先被第二个齿轮的逆时针转动所证明，而后又被第三个齿轮的顺时针转动所证明。由于写下正确的图形类型，我们会得到一个树状结构（或根状结构，取决于方向），我们说正确的类型是树状证明。为了对比树状证明，第一种类型被称为类图证明。最初，Denecker和Schreye（1993）发明了树状证明，但后来Denecker等人（2015）发明了图状证明。

现在我们有足够的信息来说明本论文的第二个中心问题：这两种类型的理由在什么时候是等价的；也就是说，当且仅当一个事实有一个好的树状理由时，它就有一个好的树状的理由。这一属性被称为图式重现性，第二章中解释了它被这样称呼的原因。

研究这两个属性是本论文的中心目标。特别是，我们的目标是找到对分支评价的限制，使这些属性成立。此外，这些属性是未来新的证明语义的准则。如果新的证明语义被设计出来，它应该满足这两个属性才有实际用途，因为第一个属性确保语义不矛盾，而第二个属性允许将树状证明压缩成图状证明。这在实际的计算机应用中有着重要的影响，因为大多数时候，树状的理由是一个无限的结构，因此不适合放在内存中。因此，如果有一个同样好的类似图的理由，那么就可以用它来代替。例如，理由被用于奇偶性博弈求解器中，见Lapauw等人（2020）的工作。

有点出乎意料的是，这些属性在本质上是相互关联的：如果类图证明是一致的，那么图的可重复性就成立，树状证明也是一致的。

除了这两个属性之外，我们还有两个额外的研究方向。如前所述，论证理论旨在成为一个统一的框架。另一个起源于逻辑编程的框架是AFT。AFT的基础在于Tarksi的fixpoint理论（Tarski, 1955）；因此AFT的基本对象是运算符和它们的fixpoint。由于逻辑论证和AFT捕获之间存在重叠，这就引出了这两种形式主义之间的关系问题。

我们最后的研究方向是关于知识表示的模块化。为了拥有高效的知识表征，最重要的是，如果增加了新的逻辑构造，语义学就不需要完全被改造来获得它的工作。也就是说，知识表示应该是可组合的。Denecker等人（2015）提供了一种通过嵌套理由框架来组合不同理由语义的方法。然而，为了赋予嵌套以意义，它被压缩到常规的辩解语义。这样做，在理由中失去了很多信息，其效果是，理由没有一个合适的解释特征。因此，这就提出了一个问题：我们是否可以通过提供另一种方法来改善嵌套，而不丢失理由中的信息。