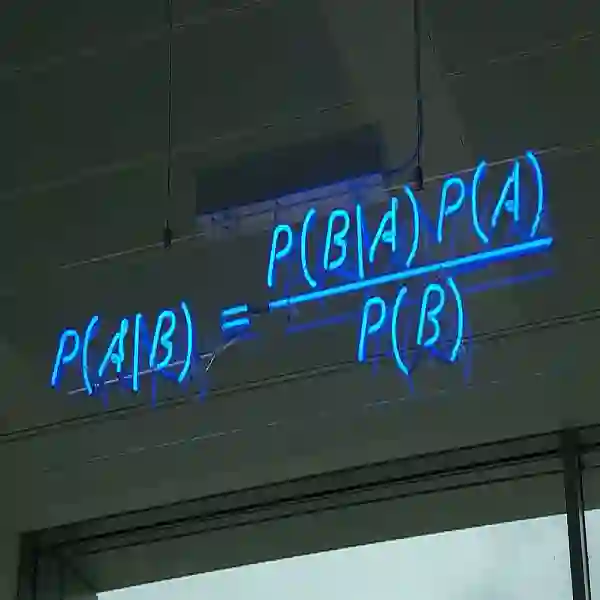图深度学习与贝叶斯如何结合？Errica博士论文《 图贝叶斯深度学习》阐述方法框架，附201页pdf与Slides

作者介绍

Federico Errica在比萨大学获得计算机科学博士学位，导师是Alessio Micheli和Davide Bacciu。他现在是NEC欧洲实验室有限公司的研究科学家。他的研究兴趣包括图形的深度概率模型、神经网络和混合架构。

Bayesian Deep Learning for Graphs

**结构化数据的自适应处理是机器学习中一个长期存在的研究课题，**研究如何自动学习从结构化输入到各种性质的输出的映射。最近，人们对图形的自适应处理越来越感兴趣，这导致了不同的基于神经网络的方法的发展。**在本论文中，我们采用不同的方法，提出了一个用于图学习的贝叶斯深度学习框架。本论文首先回顾了该领域中大多数方法建立的原则，然后对图分类再现性问题进行了研究。然后，通过以增量的方式构建我们的深度架构，我们继续将深度学习的基本思想与贝叶斯世界联系起来。这个框架允许我们考虑具有离散和连续边缘特征的图，产生足够丰富的无监督嵌入，以达到在多个分类任务上的先进水平。该方法还支持贝叶斯非参数扩展，它可以自动选择几乎所有模型的超参数。两个真实世界的应用证明了深度学习对图形的有效性。第一个问题是用有监督的神经模型预测分子模拟的信息理论量。**之后，我们利用贝叶斯模型来解决恶意软件分类任务，同时对过程内代码混淆技术具有鲁棒性。最后，我们试图将神经和贝叶斯世界的精华融合在一起。由此产生的混合模型能够预测以输入图为条件的多模态分布，因此能够比大多数工作更好地模拟随机性和不确定性。总的来说，我们的目标是为图深度学习的研究领域提供一个贝叶斯视角。

**https://www.zhuanzhi.ai/paper/b323bf6a83ab7fa0e026ef63a6cb988e

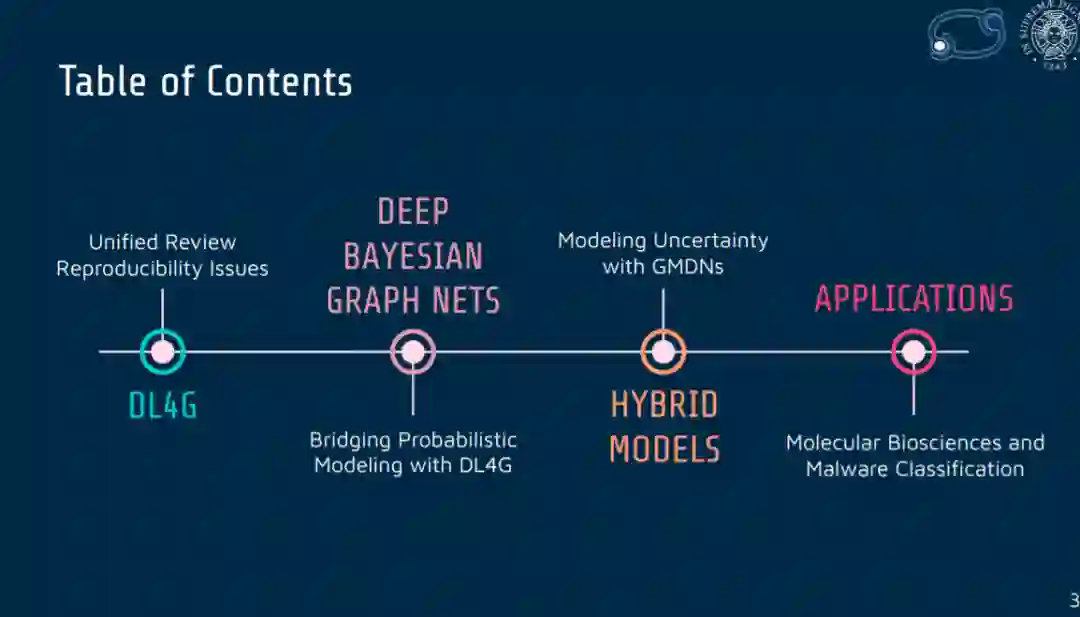
目录内容

在第二章中，我们首先回顾了概率论、贝叶斯学习的基本定义，以及我们将在接下来的工作中得到启发的模型。然后，我们将讨论图的正式定义，从而引导读者了解最常用的数学符号。最后，我们将简要总结不直接属于深度学习的图的自适应处理的相关方法。

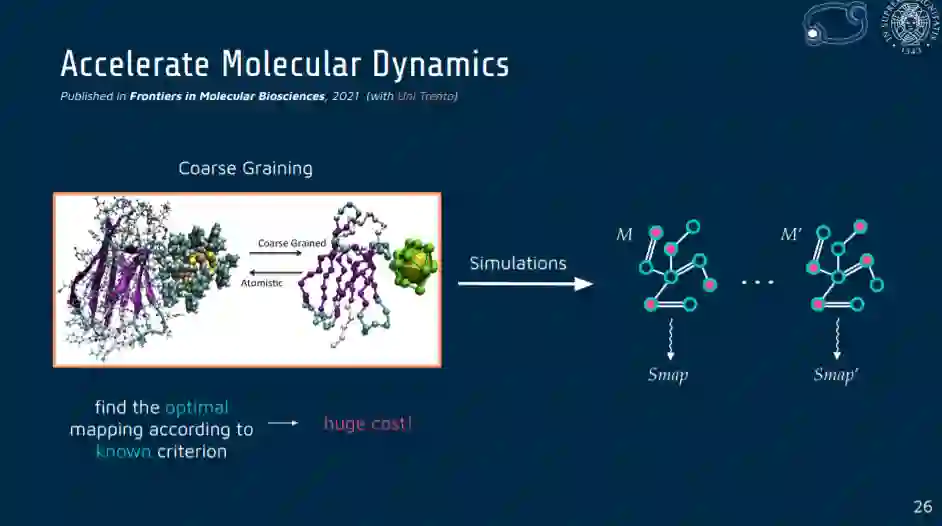
在第三章中，我们介绍了机器学习图的基本原理，不管模型的性质如何，可以是神经模型、概率模型或混合模型。我们以一个分子生物科学领域的应用来结束本章。

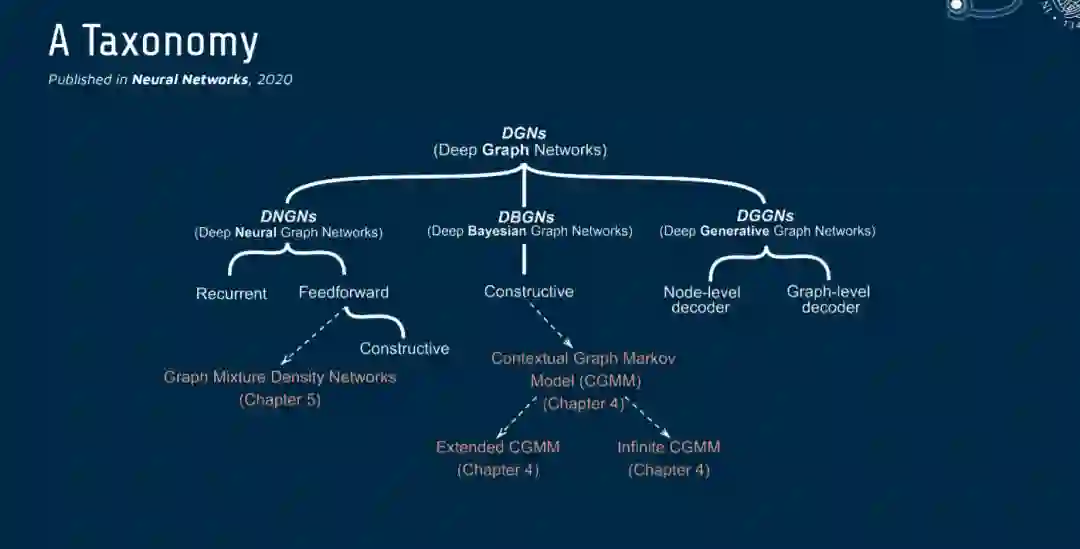
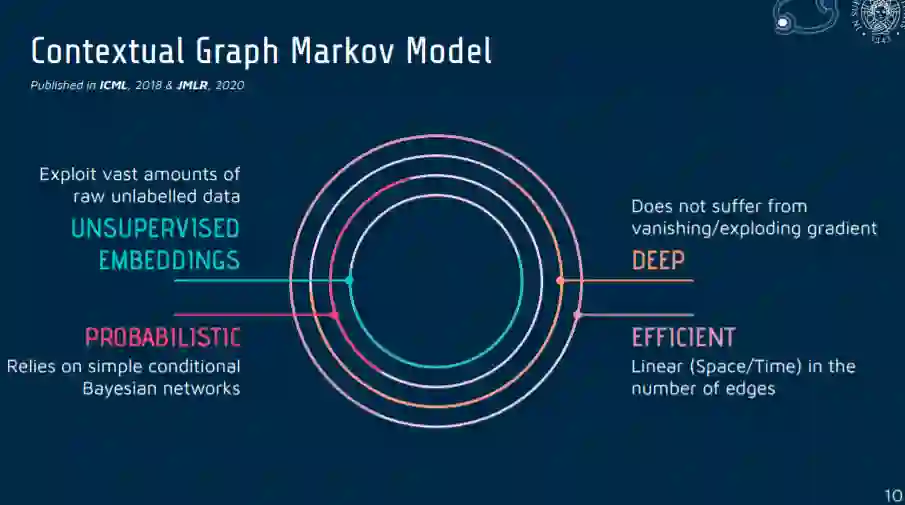
在第四章中，我们介绍了本论文在方法论上的主要贡献，即深度贝叶斯图网络。这篇论述的组织方式是，新技术可以被看作是以前技术的扩展，许多并行性与第三章的基本概念相一致。对于提出的每个模型，我们将展示各种各样的实证分析，以支持基准的结果。在本章的最后，我们将所开发的模型应用于一个真实世界的恶意软件分类任务。

在第五章中，我们利用神经网络和概率网络的优点，设计了一个混合模型，称为图混合密度网络，以输出任意输入图的多模态分布。对合成随机图和真实世界的化学任务的经验评估是为了表明，对于某些问题，图深度学习的“标准”方法不能产生正确的输出。

第六章对论文进行了总结，讨论了有待解决的问题和未来的研究方向。