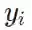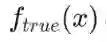![]()
本文为约6200字,建议阅读12分钟
本文介绍了深度“神经”与传统机器学习模型的不同之处。
今天与大家分享的是深度神经网络的工作方式,以及深度神经与“传统”机器学习模型的不同之处。我的计划具体如下:
-
-
接下来回顾偏差-方差分解,并在偏差-方差权衡的背景下,在VC-维数和非参数上进行探讨;
-
-
在文末做一个非常简单的实验,用图形直观地讲解为什么双下降现象会发生。
首先从数据开始。假设我们标记了数据,即是满足Px,y分布的输入数据x(比如图片)和标签y。
-
分布Px,y固定且未知。对于i = 1……N来说,可获得样本
![]() ,
,
![]() 。
。
-
-
通常来说,我们需要假设标签y和输入x间有y=
![]() 的函数关系,即是说,标签是精确的、没有歧义的,但并非总是如此。
的函数关系,即是说,标签是精确的、没有歧义的,但并非总是如此。
我们想要“训练”的是某些函数f:x↦y ,或者说是更普遍地估计条件分布P(y∣x)。我们的候选函数来自于参数集F={fθ∣θ∈Θ},在这里θ 代表参数。
为了达成目标,我们设定了损失函数(或风险函数),从概念上讲,我们希望将预期损失
![]() 最小化。
最小化。
第一次尝试通常是将经验风险或者经验损失
![]() 最小化。如果我们的损失函数是负对数似然,将
最小化。如果我们的损失函数是负对数似然,将
![]() 最最小化就意味着计算最大相似估计。
最最小化就意味着计算最大相似估计。
对偏差-方差分解和偏差-方差平衡的简单介绍
对于最小二乘损失L=(f(x)−y)2(最基本的回归估计量)来说,把预期损失分解成几个部分是很容易的。其诀窍在于,我们需要意识到我们的训练数据本身是一个从n次乘积分布
![]() 中采得的随机变量,且我们训练的模型 f依赖于D,记作
中采得的随机变量,且我们训练的模型 f依赖于D,记作
![]() 。通过巧妙地添加
。通过巧妙地添加
![]() 并利用 (x,y) 和D的独立性,我们可以将预测的期望平方误差分解为:
并利用 (x,y) 和D的独立性,我们可以将预测的期望平方误差分解为:
现在为了得到我们预测的良好的预期平方误差,我们必须注意到模型输出的偏差(第一项)和方差(第二项)的和很小。注意这里所有的项都是非负的。
针对二元分类器的预期精度,其实存在着类似但更复杂的分解,但其他损失函数通常很难分解,尽管我们可以想象那样的模型选择的工作也是类似的。
因为让偏差/方差等于0或非常接近0都相对容易,这样分解会让我们在偏差和方差间做出权衡:通过使用D中每个数据点的样本均值作为估计,偏差可以非常小,且能巧妙地给出正则性论证来假设函数是Lipschitz函数或至少是一致连续。这就是极端的过拟合。通过预测不依赖于D的函数,比如
![]() ,我们可以让方差为0,这样则是极端的欠拟合。
,我们可以让方差为0,这样则是极端的欠拟合。
请注意,均方误差的偏差-方差分解是一个根据数学定理(或至少一个引理)成立的方程,所以是普遍适用的,不需要任何条件。
从某种程度上说,从上述极端情况转向更温和的条件也表明了我们在实践中可以做些什么。
增加候选函数的集合
一种方法是,以一组非常严格的函数作为候选函数,然后有意义地扩大候选函数的空间,以获得(假设是嵌套的)序列F0⊂F1⊂…. 关键想法是,进一步研究可以让模型更好地适应数据,而我们则须知道何时停止这种深入。Vapnik和Chervonenkis 的结构风险最小化原理就是这么做的,尽管该原理没有使用偏差-方差分解,而是使用了预期损失(风险)与D上的观察损失(经验风险)的边界,和一个依赖于训练数据集大小N 和函数集
![]() 的大小或其VC维的项。此处的典型情况是,一个人想要N≥VC-dim个样本,却可能有N≤20VC-dim个样本。但请注意,这里参数的数量不是标准的一部分(但可能会影响VC维)。
的大小或其VC维的项。此处的典型情况是,一个人想要N≥VC-dim个样本,却可能有N≤20VC-dim个样本。但请注意,这里参数的数量不是标准的一部分(但可能会影响VC维)。
最后,传统标准比如赤池信息量准则尝试告诉你应该“投资”多少参数来达到低的负对数可能性。但是Bishop在其引言中发现,这些方法并不是很有效。
非参数估计:正则化
经典的非参数估计从另一个极端开始。如果我们取某个函数空间,如在
![]() 里有弱导数的索伯列夫函数空间
里有弱导数的索伯列夫函数空间
![]() (无论采用何种测度,是x的分布抑或是包含输入的
(无论采用何种测度,是x的分布抑或是包含输入的
![]() 的勒贝格测度),我们可以匹配任意有限样本D上每一点的样本均值,从而可以获得0点态偏差, 但是最小化经验风险是病态的,有无限多的解。
接下来要做的就是正则化。最著名的例子可能是增加一个规范项从而导致Tikhonov正则化,所以我们的损失看起来会是这样:
如果我们从偏差-方差的角度来看,我们能够平衡偏差(当λ→0没有偏差,但会导致病态)与方差(当λ→∞,我们处于
的勒贝格测度),我们可以匹配任意有限样本D上每一点的样本均值,从而可以获得0点态偏差, 但是最小化经验风险是病态的,有无限多的解。
接下来要做的就是正则化。最著名的例子可能是增加一个规范项从而导致Tikhonov正则化,所以我们的损失看起来会是这样:
如果我们从偏差-方差的角度来看,我们能够平衡偏差(当λ→0没有偏差,但会导致病态)与方差(当λ→∞,我们处于
![]() 。我们并不想让方差为0,因为我们的正则化项仅仅是一个半范数)。当然了,Grace Wahba有关正则化回归的研究尤其与保持偏差-方差间的良好平衡相关,特别是与如何寻找到一个合适的λ值相关。
通过观察给定的λ,
。我们并不想让方差为0,因为我们的正则化项仅仅是一个半范数)。当然了,Grace Wahba有关正则化回归的研究尤其与保持偏差-方差间的良好平衡相关,特别是与如何寻找到一个合适的λ值相关。
通过观察给定的λ,
![]() 的极小值
的极小值
![]() 会有半范数值
会有半范数值
![]() ,该值必然能在
,该值必然能在
![]() 中将经验最小二乘损失(第一项) 最小化,就可以将前一节中的ansatz函数与嵌套空间Fi联系起来。因此来自递增权重序列
中将经验最小二乘损失(第一项) 最小化,就可以将前一节中的ansatz函数与嵌套空间Fi联系起来。因此来自递增权重序列
![]() 的递减范数序列
的递减范数序列
![]() 就给到了我们嵌套的Ansatz空间。
就给到了我们嵌套的Ansatz空间。
许多流行的正则回归方法(例如Lasso)适合这种类型的框架。
赞美VC界
让我们讲回VC 界,正式一点以便增强直觉。关键的概率界限是为了准确性(或者说0-1的风险)
我们来分析一下。外面部分称“概率大于等于1−η”(我们还得更精确一点),此处我们觉得概率η太小了,这意味着我们所有的只是一个概率界限,而不是一个“几乎肯定”的保证。
内部的部分基本上是说,在全概率分布上的精度非常接近于在训练集上的精度,也就是说在N变得非常大的时候,我们有一个差值趋于零的精确边界。
从表面上看,这告诉了我们关于风险或准确性的信息,但是关于模型又说明了什么呢? 在我看来,关键的信息是,我们的模型是如此严格,以至于我们可以看到测试集上发生的一切(或者更精确地说,在完整的Px,y分布上发生的一切)已经在训练集中发生了。
贝叶斯放一边
在贝叶斯环境下,正则化可以被解释为最大后验(MAP)估计,或者——如果我们经历了定义先验的麻烦——我们也可以对所有f∈F的估计进行积分。
当我们将model.parameters()(这里我用的是PyTorch)传递给优化器时,深度学习看起来好像是参数化的。但其实它不是!
看起来这种正则化方法正是深度学习运作的理论框架——有时人们对此知之甚少。我们的模型足够大,从“道德上看来”足以成为非参数,尽管我们还没有完全理解,但我们所做的大多数事情(比如augmentation, norm layers和 dropout)其实都是正则化。
这也是M. Belkin等人所写的《协调现代机器学习实践和偏差-方差权衡》(Reconciling modern machine learning practice and the bias-variance trade-off)的主题和他们早期研究的主题,即泛化性能的关键是由某个特定函数空间范数衡量的函数的规律性或平滑性。
我们有必要仔细看看M. Belkin等人(我认为这是首次)对双下降现象的描述:
-
M. Belkin等人把条件中的“传统(classical)”和“现代(modern)”等限定词用引号括了起来。“现代”条件是一种十分之非参数的学习,具有一种我们还需要更加深入理解的正则化。
-
在多参数的条件下,偏差-方差思维似乎仍然是完全适用的,但非参数回归可能是比“限制容量”的候选集更好的参考框架。
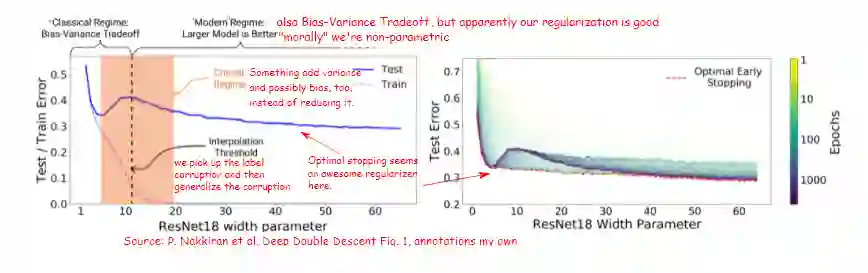
对于双重下降现象的普遍理解似乎都是基于P. Nakkiran等人的文章:《双重下降》(Deep Double Descent),这证明了这篇论文的优秀,也证明了OpenAI能够将这些选题推介给更广泛的受众。他们用更真实的网络进行了系统的实验(M. Belkin等人则引用了更浅层的网络)。对我来说,一个重要的结论是,双重下降现象在标签损坏的两种实验条件中存在“凹凸”,他们的报告称,在标签干净的实验中,所得到的结果则要平缓得多,没有那么“凹凸”。
他们给出了一张图,这张图显示了对于固定次数的epoch,用损坏标签将一个修改过的ResNet18训练成CIFAR10这个过程中的测试错误。修改是指信道数量降到原数量的k分之一(k在64到1这个范围)(意思是他们会从原ResNet18的64分之一开始做实验,逐渐增加,最后达到原数量)。标签损坏发生在数据集中(在某一次epoch,而不是每个epoch中),15%的标签被切换到一个随机错误的类。这被解释为一种概略的误设。
04. VC理论对于用噪声标签拟合模型有什么启示?
通过上面的讨论,我们了解到当一个模型处于VC界有用的限定条件中(比如当小模型处于“传统”条件中),如果训练数据 D来自与原始数据相同的分布 Px,y,测试集的测试精度(很可能)接近训练精度。换句话说,这个条件意味着我们假设Px,y有相同的损坏程度(和损坏种类)。但这意味着如果模型学习了,且学会了不被损坏的训练数据分散太多注意力,也就是说,在训练数据上,正确标签会挤出损坏标签。
让对深度学习的直觉化变得困难的原因之一是Ansatz领域的自适应特性。我这么说的意思是,我们没有一个固定的特征提取器(由手动构造,并由核机中使用的核家族给出)将学习应用到特征上。通常,我们将最后一层的输入视为特征(通过word2vet式损失、原型网络、基准无监督学习等方式学习的向量表示方法),或者我们可能在MLP分类器头之前的卷积层末尾分割卷积网络。
传统的做法是将学习后的分类器放在固定的特征提取器上,E. Hoffer等人的想法却相反,他们甚至建议对分类器进行固定,即只对特征提取器进行训练。
因此,我们可能会试图通过假装提取特征来简化我们的直觉。在P. Nakkiran等人的标题图片实验中,当使用t-SNE等降维机制将通过无噪声数据学习到的特征可视化时,添加标签噪声相当于在每个类对应的点的blob上添加噪声。考虑到这一点,我们可以进行一个类似的实验,这个实验甚至比M. Belkin等人的人工数据实验更简单,那就是:理解深度学习。
撇开统计数据不谈:下文推测了一些可能发生的情况,通过想象我们可以在原型网络中得到与P. Nakkiran等人图中所描述的相同的现象,且容量由我们所能拥有的原型数量来表示:
-
在最左边width(参数)值1到5附近,我们的原型比类少,模型拟合程度不高(欠拟合),因为模型不能代表所有的类。
-
在width5附近,我们有10个(或者适当地更多)原形,但是,在每一个原型的训练中损坏标签都被挤出了,所以这些损坏标签没有发挥作用。
-
在width5到10这个范围,原型收集损坏的标签。由于每个原型都有一个用在推断阶段的“影响范围”,所以存在一个相当大的空间,在这个空间中损坏原型与测试是非常相关的。
-
在width10以外的范围,我们增加了更多的原形。原型之间变得更近,在推断阶段中损坏的标签原型也被“挤出”,因此它们的“影响范围”就会变得更小(因为比起拥有3个损坏原形,同一个类拥有5个非损坏原型中的3个的概率更大)。
这对偏差-方差分解意味着什么? 回想一下,分解在空间上是逐点的,并像之前一样要对各种训练数据集进行方差和偏差处理。假设你只有两个类,那么预测和标签要么是0要么是1。接下来原型收集已损坏的标签,就会产生偏差(因为你将以某种概率预测错误的事情)和方差(因为糟糕预测的区域取决于哪些标签已损坏,也就是取决于我们在哪个数据集D上绘制),并使错误预测的区域更小,从而减少方差和偏差。
在这种直觉中,
早期停止的作用是检测模型何时开始收集已损坏的标签
。
所以看起来现代神经网络本质上是非参数的,其工作方式依赖于各种正则化。为了使用M. Belkin等人的公式,我们希望更加了解,我们对于各种技术如何对某些函数空间范数作用的理解到了什么程度。似乎很难得出“传统”统计数据表明现代学习不起作用的结论。
Hastie等人的《高维无脊最小二乘插值中的惊喜》(Surprises in High-Dimensional Ridgeless Least Squares Interpolation)一文将最小二乘作为模型问题,提供了非常全面的分析,这也可能为深度学习现象提供直觉。
在插值条件中挤出错误标记的数据
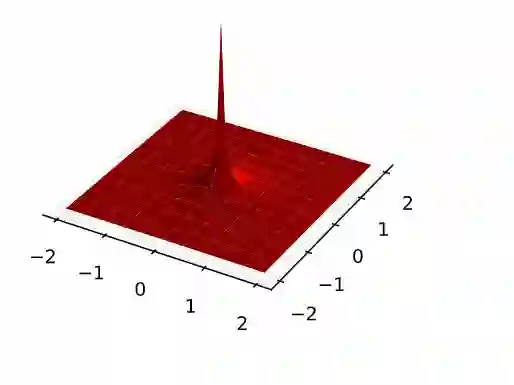
我们可以做一个非常简单的插值条件的模拟。我们来思考一个由2d标准单位法线提取并沿着水平轴移动±2的点的二分类问题,并从每个类别的分配中抽取25%的点。
为了得到一个插值条件,我们使用一个具有明显峰值的核。为了有一个易分析处理的质量并将其标准化为1,我们使用核
这个核有单位质量,在x=0时趋于无穷,且从原点衰减:
这意味着,如果我们将每一类的密度表示为样本
![]() 处核的均值,即:
处核的均值,即:
假设不同类别的点不重合(几乎肯定如此),我们可以根据
![]() 更大的点对每个点进行分类,或者说,如果我们想通过标准化每个点的概率密度来获取概率
更大的点对每个点进行分类,或者说,如果我们想通过标准化每个点的概率密度来获取概率
这给了我们一个插值解——在每个训练点,标签类有无限密度,所以它被归类为属于这个类。
那么标签错误发生了什么呢? 标签错误会导致损坏的训练点附近的某些区域被分配给错误的类。然而,附近正确类的点越多,错误分类的区域就越小。我们可以交互地尝试。随着点数的增加,测试误差会减少。
这意味着什么呢? 这说明对于插值解,在测试时间内,良好的训练点会挤出标记糟糕的点。
对抗示例
但是,随着数据的增加,当坏分类的区域和被随机抽样的数据点击中的概率减小时,随机抽样点到下一个坏样本的距离也减小了。这意味着除了利用模型的不良连续性(即输入的小变化会导致提取的特征发生大的变化),插值条件也能使对抗例子更容易产生,因为我们只需要特征的小变化。
特征噪声类似于标签噪声
但是,双重下降不是也发生在没有损坏标签的情况下吗? 我们“仅仅”需要格外小心地处理我们的训练数据吗?
好吧,没这么简单。高维特征在本质上可能比低维特征噪声更多:想象一下在高维空间(比如d)中有一个两类线性分类。我们有了有向量
![]() 和偏差
和偏差
![]() 的分类器。给定输入
的分类器。给定输入
![]() ,当x⋅v+b≥0时,类为1;否则,类为0。如果我们预先知道输入是有界的,我们可以找到类原型
,当x⋅v+b≥0时,类为1;否则,类为0。如果我们预先知道输入是有界的,我们可以找到类原型
![]() ,并使用距离
,并使用距离
![]() 进行分类。但随后的线性分类器的d−1维零空间(null-space)中的向量,比如我们可以添加到输入中而不改变结果的向量空间
进行分类。但随后的线性分类器的d−1维零空间(null-space)中的向量,比如我们可以添加到输入中而不改变结果的向量空间
![]() ,可能对这个距离有很大帮助,从而使得
,可能对这个距离有很大帮助,从而使得
![]() 成为对更相关的投影距离
成为对更相关的投影距离
![]() 的一个噪声估计。
如果我们想保持在二维空间,我们可以放大噪声维度。这就将我们引入第二个实验。我们来绘制独立的随机二维点,其在“特征维度”中的标准偏差为0.5,在“噪声维度”中的标准偏差为5。这两个类用±1分开。我们使用EM算法来将每个维度的标准偏差为1的K高斯函数的混合值拟合到每个类中。通过比较两个拟合密度进行分类。我们使用5000个训练点和1000个测试点。
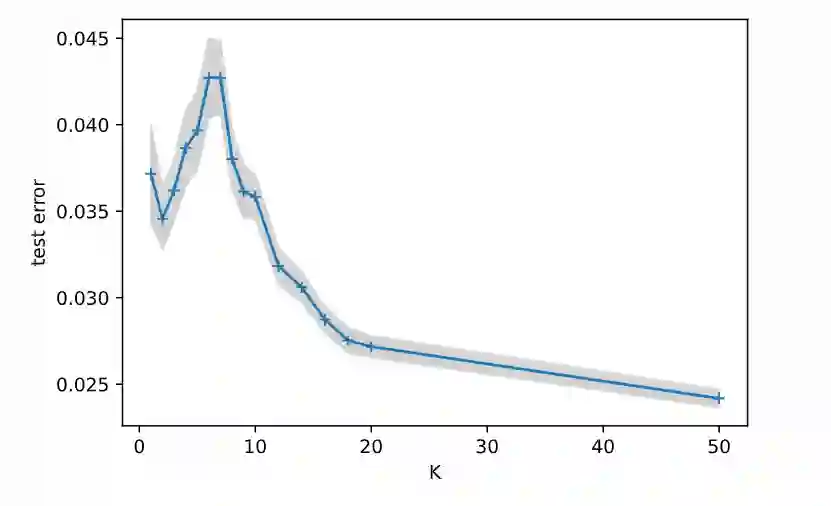
如果我们以不同的K值运行200次,并记录其准确性,我们可以看到双重下降中的凹凸:
关于这些实验的一个问题是:误差分布是倾斜的:我们得到的很多测试误差在2-3左右出现,可误差在10左右还出现了一个尾巴。这条差拟合的曲线尾部的质量随分量K的数量而变化,似乎是造成中间K的平均误差出现凹凸的主要原因。
的一个噪声估计。
如果我们想保持在二维空间,我们可以放大噪声维度。这就将我们引入第二个实验。我们来绘制独立的随机二维点,其在“特征维度”中的标准偏差为0.5,在“噪声维度”中的标准偏差为5。这两个类用±1分开。我们使用EM算法来将每个维度的标准偏差为1的K高斯函数的混合值拟合到每个类中。通过比较两个拟合密度进行分类。我们使用5000个训练点和1000个测试点。
如果我们以不同的K值运行200次,并记录其准确性,我们可以看到双重下降中的凹凸:
关于这些实验的一个问题是:误差分布是倾斜的:我们得到的很多测试误差在2-3左右出现,可误差在10左右还出现了一个尾巴。这条差拟合的曲线尾部的质量随分量K的数量而变化,似乎是造成中间K的平均误差出现凹凸的主要原因。
-
在我看来,噪音需要在推断阶段而不是在训练阶段挤出特征,由此我们看出深度学习模型的本质是非参数的。这与KDE实验非常接近。
-
即使我们有很好的标签(你有的,对吧?),深度学习中的高特征维度会导致特征中的噪音,而这些噪音的行为与标签中的噪音类似。
https://lernapparat.de/statistics-deep-learning-nonparametric

,
。
的函数关系,即是说,标签是精确的、没有歧义的,但并非总是如此。
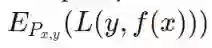 最小化。
最小化。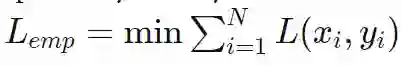 最小化。如果我们的损失函数是负对数似然,将
最小化。如果我们的损失函数是负对数似然,将
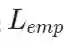 最最小化就意味着计算最大相似估计。
最最小化就意味着计算最大相似估计。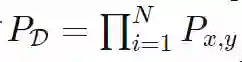 中采得的随机变量,且我们训练的模型 f依赖于D,记作
中采得的随机变量,且我们训练的模型 f依赖于D,记作
 。通过巧妙地添加
。通过巧妙地添加
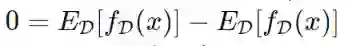 并利用 (x,y) 和D的独立性,我们可以将预测的期望平方误差分解为:
并利用 (x,y) 和D的独立性,我们可以将预测的期望平方误差分解为: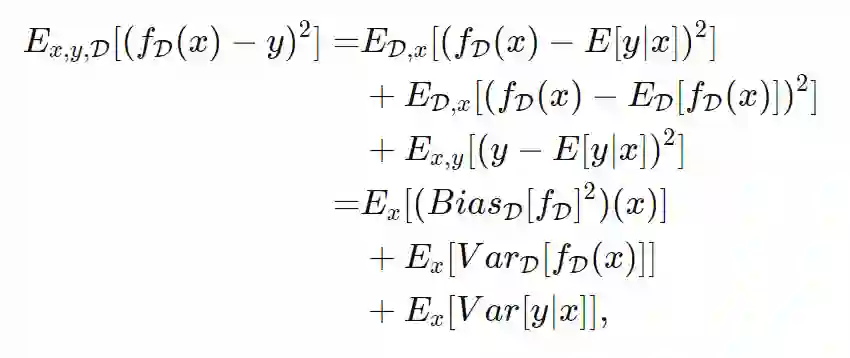
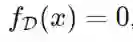 ,我们可以让方差为0,这样则是极端的欠拟合。
,我们可以让方差为0,这样则是极端的欠拟合。 的大小或其VC维的项。此处的典型情况是,一个人想要N≥VC-dim个样本,却可能有N≤20VC-dim个样本。但请注意,这里参数的数量不是标准的一部分(但可能会影响VC维)。
的大小或其VC维的项。此处的典型情况是,一个人想要N≥VC-dim个样本,却可能有N≤20VC-dim个样本。但请注意,这里参数的数量不是标准的一部分(但可能会影响VC维)。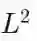 里有弱导数的索伯列夫函数空间
里有弱导数的索伯列夫函数空间
 (无论采用何种测度,是x的分布抑或是包含输入的
(无论采用何种测度,是x的分布抑或是包含输入的
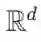 的勒贝格测度),我们可以匹配任意有限样本D上每一点的样本均值,从而可以获得0点态偏差, 但是最小化经验风险是病态的,有无限多的解。
的勒贝格测度),我们可以匹配任意有限样本D上每一点的样本均值,从而可以获得0点态偏差, 但是最小化经验风险是病态的,有无限多的解。

 。我们并不想让方差为0,因为我们的正则化项仅仅是一个半范数)。当然了,Grace Wahba有关正则化回归的研究尤其与保持偏差-方差间的良好平衡相关,特别是与如何寻找到一个合适的λ值相关。
。我们并不想让方差为0,因为我们的正则化项仅仅是一个半范数)。当然了,Grace Wahba有关正则化回归的研究尤其与保持偏差-方差间的良好平衡相关,特别是与如何寻找到一个合适的λ值相关。
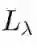 的极小值
的极小值
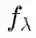 会有半范数值
会有半范数值
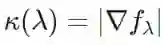 ,该值必然能在
,该值必然能在
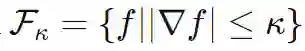 中将经验最小二乘损失(第一项) 最小化,就可以将前一节中的ansatz函数与嵌套空间Fi联系起来。因此来自递增权重序列
中将经验最小二乘损失(第一项) 最小化,就可以将前一节中的ansatz函数与嵌套空间Fi联系起来。因此来自递增权重序列
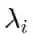 的递减范数序列
的递减范数序列
 就给到了我们嵌套的Ansatz空间。
就给到了我们嵌套的Ansatz空间。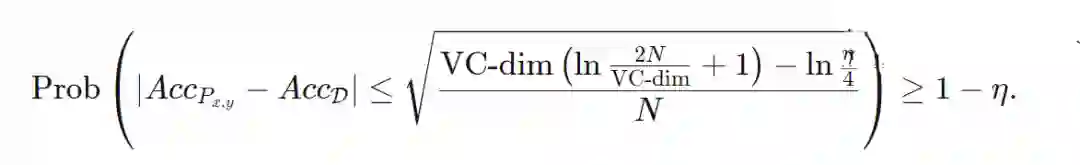


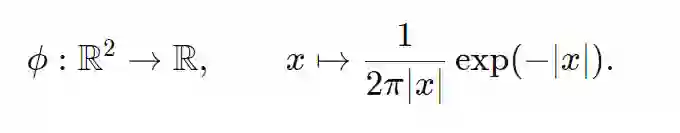
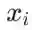 处核的均值,即:
处核的均值,即: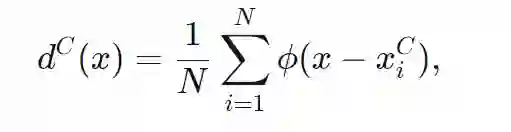
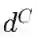 更大的点对每个点进行分类,或者说,如果我们想通过标准化每个点的概率密度来获取概率
更大的点对每个点进行分类,或者说,如果我们想通过标准化每个点的概率密度来获取概率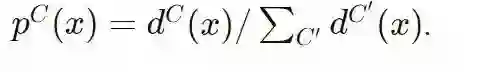

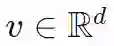 和偏差
和偏差
 的分类器。给定输入
的分类器。给定输入
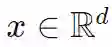 ,当x⋅v+b≥0时,类为1;否则,类为0。如果我们预先知道输入是有界的,我们可以找到类原型
,当x⋅v+b≥0时,类为1;否则,类为0。如果我们预先知道输入是有界的,我们可以找到类原型
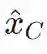 ,并使用距离
,并使用距离
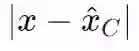 进行分类。但随后的线性分类器的d−1维零空间(null-space)中的向量,比如我们可以添加到输入中而不改变结果的向量空间
进行分类。但随后的线性分类器的d−1维零空间(null-space)中的向量,比如我们可以添加到输入中而不改变结果的向量空间
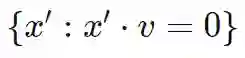 ,可能对这个距离有很大帮助,从而使得
,可能对这个距离有很大帮助,从而使得
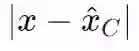 成为对更相关的投影距离
成为对更相关的投影距离
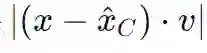 的一个噪声估计。
的一个噪声估计。