WWW24 | 赋予预训练图模型可证明的公平性

Endowing Pre-trained Graph Models with Provable Fairness

作者：张中健，张梦玫，于越，杨成，刘佳玮，石川 单位：北京邮电大学 前言：预训练的图模型（PGMs）在图机器学习领域受到广泛关注，它们通过捕捉可转移的固有结构属性并将其应用于不同的下游任务。与预训练语言模型类似，PGMs 也会继承来自人类社会的偏见，导致在下游应用中出现歧视行为。现有公平性方法的去偏过程通常与 GNNs 的参数优化耦合。然而，现实中不同的下游任务可能与不同的敏感属性相关联，直接采用现有方法来提高 PGMs 的公平性既不灵活也不高效。此外，大多数现有去偏方法缺乏理论上的保证，即模型预测的公平性缺乏可证明的下限，无法直接在实际场景中提供保证。为了解决上述问题，我们提出了一个新颖的框架，赋予预训练图模型可证明的公平性（称为 GraphPAR）。GraphPAR 在下游任务中冻结 PGMs 的参数并训练一个参数高效的适配器来灵活提高 PGMs 的公平性。具体来说，我们在节点表示上设计了一个敏感语义增强器，为每个节点扩展不同敏感属性语义的节点表示。扩展的表示将直接用于优化适配器的参数，防止敏感属性语义从 PGMs 传播到任务预测。同时，通过GraphPAR，我们可以量化每个节点的公平性是否可证明，即在一定的敏感属性语义范围内预测总是公平的。在真实世界数据集上进行的大量实验评估表明，GraphPAR 在节点分类任务上实现了最先进的性能和公平性。此外，基于 GraphPAR，大约 90% 的节点具备可证明的公平性。

一、介绍

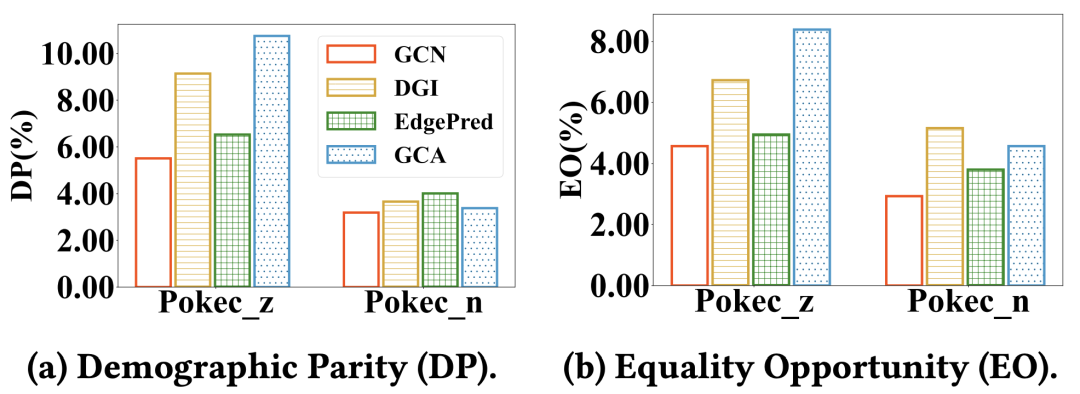
图神经网络（GNNs）在分析图结构数据方面取得了巨大的成功，例如社交网络和网页网络。最近，受预训练语言模型的启发，各种预训练图模型（PGMs）被提出。一般来说，PGMs 在预训练阶段通过无监督学习范式捕获可转移的固有图结构属性，然后通过微调来适应不同的下游任务。作为一种强大的学习范式，PGMs 在图机器学习领域受到了相当多的关注，并广泛应用于推荐系统和药物发现等各个领域。 然而，最近的研究表明，预训练的语言模型往往会继承预训练语料库的偏见，这可能会针对性别、种族和宗教等敏感属性产生有偏见或不公平的预测。基于相同的训练范式，针对 PGMs 提出以下问题：预训练的图模型是否也继承图上的偏见？为了回答这个问题，我们在数据集 Pokec_z 和 Pokec_n上评估了三种不同 PGMs 的节点分类公平性，结果如图 1 所示。我们观察到 PGMs 比普通 GCN 更不公平。这是因为 PGMs 在预训练阶段能很好地捕获图上的语义信息，其中不可避免地包含敏感的属性语义。进一步的问题自然而然地出现：如何提高 PGMs 的公平性？解决这个问题非常关键，特别是在基于图的高风险决策场景中，例如社交网络和候选人工作匹配，因为有偏见的预测会引发严重的道德和社会问题。

图1：在 Pokec_z 和 Pokec_n 数据集上评估 PGMs 的节点分类公平性。 DP和 EO报告了三种 PGMs（即 DGI、EdgePred、GCA)和GCN的公平性。

尽管近年来已经提出了公平 GNNs 的实质性方法，但直接使用它们来提高 PGMs 的公平性是不灵活且低效的，即大多数现有工作通常都会针对特定任务训练公平的 GNNs。例如，基于反事实公平性的方法通过构建不同的反事实训练样本来训练公平的 GNNs 编码器。使用敏感属性分类器的方法通过在训练阶段引入对抗性损失来限制 GNNs 捕获敏感语义。显然，上述方法的去偏过程与 GNNs 的参数优化是耦合的。然而，在实际中，相同的 PGMs 可以用于不同的下游任务，并且不同的下游任务可能与不同的敏感属性相关联。在预训练阶段针对特定任务进行去偏不灵活，并且为每个任务维护特定的 PGMs 效率低下。此外，大多数现有的公平性方法缺乏理论分析和保证，这意味着它们没有提供实际的保证，即模型预测公平性的可证明的下界，这对于确定是否在实际场景中部署模型具有重要意义。

在本文中，我们试图通过提出 GraphPAR 来解决上述问题，这是一种新颖的适配器调优框架，可以高效、灵活地赋予 PGMs 可证明的公平性。具体来说，在下游任务中，我们首先冻结 PGMs 的参数，然后在节点表示上设计敏感语义增强器，为每个节点扩展具有不同敏感属性语义的节点表示。扩展表示将直接用于训练适配器，以便适配器处理后的节点表示独立于敏感属性语义，防止敏感属性语义从 PGMs 传播到下游任务预测。此外，通过GraphPAR，我们量化每个节点的公平性是否可证明，即在敏感属性语义的一定范围内预测总是公平的。例如，当一个人的性别语义逐渐从男性过渡到女性时，我们的可证明公平性保证了预测结果不会发生改变。综上所述，GraphPAR 可以适用于任何 PGMs，同时在理论上保证公平性。我们的主要贡献可以概括如下：

1. 我们首次探讨了 PGMs 的公平性，发现 PGMs 在预训练阶段由于不可避免地捕获敏感属性语义，从而导致下游任务预测不公平。
2. 我们提出 GraphPAR 来高效灵活地赋予 PGMs 可证明的公平性。在下游任务的适应过程中，GraphPAR 利用适配器进行参数高效的适应，并利用敏感属性语义增强器来保证公平性。
3. 现实世界不同数据集的大量实验结果表明，GraphPAR 实现了最先进的预测性能和公平性。同时，在GraphPAR的帮助下，约90%的节点都具备可证明的公平性。

二、GraphPAR的实现

图2：GraphPAR 概述。在适配器调整阶段，我们首先利用PGMs获得节点表示 。然后，我们设计一个敏感语义增强器来扩展具有不同敏感属性语义的节点表示，即敏感属性样本集合。最后，扩展的节点表示直接用于训练适配器，将节点表示转换为独立于敏感属性语义。在可证明公平性阶段，基于训练有素的适配器和分类器来构造其平滑版本，我们使用平滑适配器获得其输出边界保证 ，并使用平滑分类器获得其局部鲁棒性保证 。接下来，我们通过比较 与 的大小来量化每个节点的公平性是否可证明。 我们提出了一种新颖的适配器调优框架GraphPAR，它灵活有效地提高了PGMs的公平性。首先，我们在 GraphPAR 上定义 PGMs 的公平性，要求模型预测不受节点的敏感属性语义变化的影响。接下来，为了实现公平性目标，如图2（a）适配器调优所示，GraphPAR由两个关键组件组成：（1）敏感语义增强器，它为每个节点扩展具有不同敏感属性语义的节点表示，以帮助进一步训练适配器。 (2）适配器，通过对抗性去偏方法将节点表示转换为独立于敏感属性，防止敏感属性语义从 PGMs 传播到下游任务预测。

2.1 PGMs 的公平性定义

给定一个图 和在该图上的预训练的PGM⁡ 。 GraphPAR 冻结 参数并获取节点表示 ，其中 不可避免地包含图上的敏感属性语义 ，因此我们希望利用适配器 来移除它们。GraphPAR中 PGMs 的公平性定义如下： 定义 2（PGMs的公平性）在 GraphPAR 中，PGM 、适配器 和分类器 在适应下游任务期间满足公平性，如果对于任何节点： 其中 表示节点的预测标签 。与是与节点表示 具有相同维度的两个向量，即 ，表示不同的敏感属性语义。

2.2 敏感语义增强器

敏感语义增强器为每个节点扩展具有不同的敏感属性语义的节点表示，以帮助进一步训练适配器。首先，根据图上已知的敏感属性信息和节点的表示，计算出表示敏感属性语义方向的向量 。随后，我们在 方向上为每个节点的表示进行线性插值增广，以获得敏感属性语义增强集。 其中 和 表示正样本和负样本的数量， 表示应用于敏感属性语义方向的增强范围。直观上，计算 的关键思想是利用不同组之间嵌入的平均差异来表示组之间的语义关系。做平均以获得代表群体特征并消除个体特征差异的语义嵌入，做减法用于捕获组之间的语义关系。上述方法可以沿着多个敏感属性语义向量执行插值以扩展到涉及多个敏感属性的情况。

2.3 训练适配器以提升PGMs公平性

给定任一 PGM 和敏感属性增强集 ，在 GraphPAR 中，我们采用两种对抗性去偏方法来训练适配器：随机增强对抗训练和最小-最大对抗训练。 随机增强对抗训练（RandAT）：在适配器 的训练过程中，我们从增强敏感属性集中随机选择 个样本以获得对抗训练集，即

其中表示增强范围。然后将这些选定的样本纳入适配器的训练中。优化损失可以表述如下： 其中是标记节点的集合， 是下游分类器， 是衡量预测误差的交叉熵损失。 在 RandAT 中，通过在训练过程中引入不同的敏感属性语义样本，适配器 和分类器 对敏感信息的变化变得更加鲁棒，从而减轻潜在的歧视性预测。同时，这些增强样本与原始样本共享相同的任务相关语义，这进一步帮助适配器和分类器捕获任务相关语义。 **最小-最大对抗训练（MinMax）：**与 RandAT 不同，MinMax 背后的关键思想是在每一轮中找到并优化最坏情况。我们的目标是最小化表示 与其相应的增强敏感属性语义集 之间的差异。通过确保表示与 中的表示紧密一致来实现这一目标。因此我们寻求最小化和之间的距离。 MinMax 的优化目标是最小化以下损失函数： 为了进一步确保适配器 不会过滤掉有用的任务信息，我们引入交叉熵分类损失来保证下游任务的性能： MinMax的最终优化目标如下： 其中 是平衡准确性和公平性的比例因子。

三、可证明的 PGMs 公平性适应

基于GraphPAR，我们主要讨论如何为每个节点提供可证明的公平性，即预测结果在一定范围内的敏感属性语义变化是一致的。我们将此过程分为两个关键部分，如图 2 (b) 可证明的公平性所示：（1）平滑适配器。我们使用中心平滑为适配器构造一个平滑版本，它为一定范围的敏感属性语义变化的节点表示 的输出变化提供了界限。这保证了输出结果的范围包含在以 为中心、半径为 的最小包围球内。（2）平滑分类器。我们使用随机平滑为分类器构建了一个平滑版本，它提供了针对中心 的局部鲁棒性。通过确定最小包围球内的所有点是否属于同一类，即 ，我们量化每个节点的公平性是否可证明。请注意，基于训练有素的适配器和分类器，平滑模型是通过平滑函数的不同定 义构建的。因此，构建过程不需要任何参数的训练。为了符号简单起见，接下来的部分我们省略了下标。

3.1 可证明的适应

为了保证应用适配器 后表示的输出变化范围，我们采用中心平滑来获得适配器的平滑版本 。它将表示形式 作为输入并为平滑适配器 的输出边界提供了保证，如定理 1 中所述： 定理 1（中心平滑）。让 表示适配器的平滑版本的近似值，它将表示 映射到包含至少一半点 的最小封闭球的球心 。的正式定义如下： 其中 和 分别是最小包围球的圆心和半径。然后，针对 大小为 的 扰动，我们可以以高置信度保证输出变化范围： 其中： 这里 表示应用于敏感属性语义方向的增强范围。

3.2 可证明的分类

接下来，有必要证明对该最小包围球内的所有点的预测是一致分类的。 定理 2.（随机平滑）设 为分类器，。分类器 的平滑版本 定义如下： 假设 以及 满足： 那么， 对于所有 满足 $|\mathbf{\delta}|2<d{rs}$，我们$d_{rs}$可以得到如下：< p=""></d_{rs}$，我们$d_{rs}$可以得到如下：<>

其中 表示类标签集， 是标准正态分布 的累积分布函数， 是其反函数。

3.3 GraphPAR 提供可证明的公平性

结合定理1和定理2，我们将 PGMs 的可证明公平性定义如下： 定义 3（PGMs 的可证明公平性）。给定节点表示，去偏过程满足： 其中 是 的敏感属性增强集合。通过上述两种平滑技术，PGMs 的可证明公平性自然可以通过以下定理实现： 定理 3. 假设我们有一个 PGM 、一个中心平滑适配器 和一个随机平滑分类器。对于第 个节点，如果以置信度 获得 的输出保证，并以置信度 获得 的局部鲁棒性保证 ，并且满足 ，则预测结果以置信度保证是公平的，形式化的定义如下： 关于定理3点更详细介绍请参考论文原文。

四、实验

4.1 预测性能和公平性

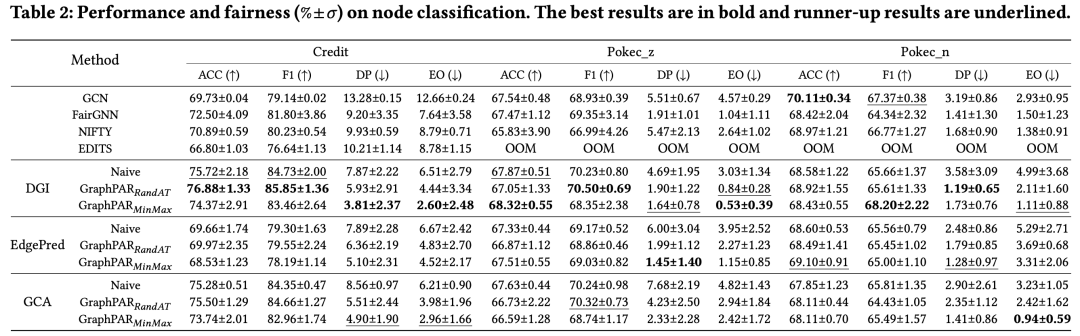
GraphPAR 在分类和公平性方面都优于基线模型。 GraphPAR 被证明在分类和公平性方面均表现出色，增强了现有的 PGMs 模型并优于其他图公平性方法。这一结果支持了 GraphPAR 在嵌入空间中解决公平性问题方面的有效性：（1）强大的预训练策略使嵌入能够包含下游任务的内在信息。（2）由于PGMs还捕获敏感属性信息，因此可以有效地构建敏感语义向量。（3）嵌入空间的增强与任务标签无关，因此，敏感的语义增强器构造的样本不会损害下游性能。 **不同 PGMs 之间 GraphPAR 的性能有所不同。**当选择不同的 PGMs 时，预测性能和公平性会有所不同。通常，我们观察到对比预训练方法 DGI 和 GCA 的性能优于预测方法 EdgePred，这意味着 GraphPAR 的性能与 PGMs 的语义捕获能力呈正相关。 **RandAT 和 MinMax 表现良好，但表现方式不同。**值得一提的是，RandAT 在分类上往往取得最好的结果，而 MinMax 在公平性上往往表现最好。训练方案的以下差异直接导致了上述结果：（1）在下游分类损失中，RandAT 利用所有增强样本，而MinMax仅利用原始样本。因此，RandAT 在分类指标 ACC 和 F1 上通常优于 MinMax。我们认为分类受益于数据增强，因为这些增强的样本与原始样本共享相同的任务相关语义，这有助于适配器和分类器进一步捕获与任务相关的语义。（2）为了对敏感信息进行去偏，MinMax最小化了敏感增强集中个体与之间的最大距离，相对于RandAT中对所有增强样本进行对抗性训练的采样策略，可以获得更好的去偏结果。 这些实证结果直接证明了 RandAT 和 MinMax 的特征。

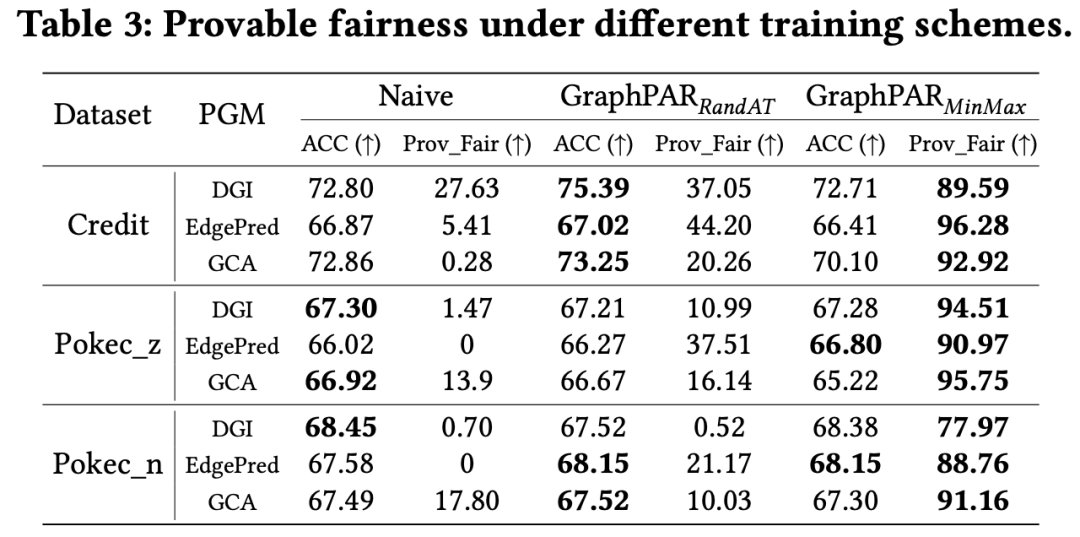
4.2 具备理论保证的可验证公平性

**与 Naive（即不加去偏处理） 表现出很少或几乎为零的可证明公平性不同，RandAT 实现了较好的可证明公平性，而 MinMax 则很好地保证了其公平性。**PGMs 的可证明公平性要求满足 < ，因为 基本相同的，但 因训练方案之间差异而有所不同：Naive 不会优化 ，因此几乎无法保证公平性； RandAT使用许多具有不同敏感属性语义的样本进行对抗性训练，对最小化有积极作用，但不是显式的； MinMax 通过直接查找和优化最坏情况来实现最佳可证明的公平性。 **RandAT 和 MinMax 的分类性能与 Naive PGMs 相比具有竞争力。**一方面，RandAT 不会损失其分类性能，因为它的增强是在敏感语义中进行的，几乎不会给任务相关信息引入噪声；另一方面，MinMax会用原始数据训练下游分类器，这意味着适配器在保证公平性的同时几乎不会对分类产生不利影响。 总之，上述结果表明，当使用 RandAT 和 MinMax 进行训练时，GraphPAR 在不影响分类性能的情况下保证了公平性。 关于敏感属性向量有效性、超参数敏感分析、高效性实验请进一步参考原文。

五、结论

在这项工作中，我们首次探索 PGMs 的公平性。我们发现 PGMs 在预训练过程中不可避免地会捕获敏感属性语义，从而导致下游任务的不公平。为了解决这个问题，我们提出GraphPAR，在下游任务的适应过程中高效灵活地赋予PGMs公平性。此外，通过 GraphPAR，我们为公平性提供了理论上的保证。真实世界数据集的大量实验证明了 GraphPAR 在实现公平预测和提供可证明的公平性方面的有效性。未来我们将进一步探索PGMs其它可信问题。 **论文链接：**http://www.shichuan.org/doc/172.pdf