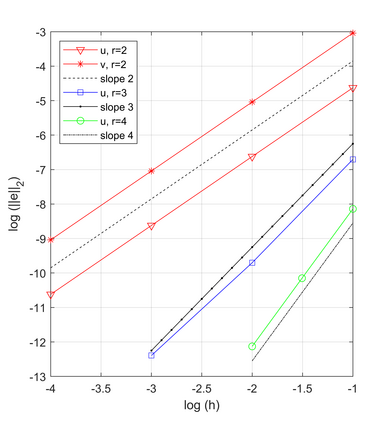
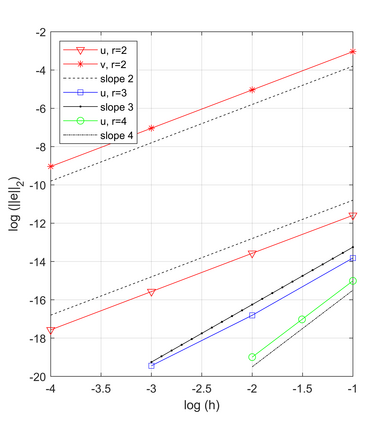
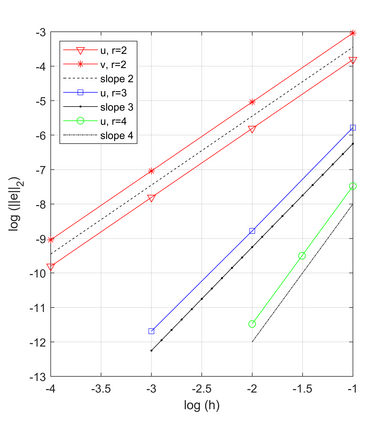
In this paper, we consider a nonlinear beam equation with the p-biharmonic operator, where $1 < p < \infty$. Using a change of variable, we transform the problem into a system of differential equations and prove the existence, uniqueness and regularity of the weak solution by applying the Lax-Milgram theorem and classical results of functional analysis. We investigate the discrete formulation for that system and, with the aid of the Brouwer theorem, we show that the problem has a discrete solution. The uniqueness and stability of the discrete solution are obtained through classical methods. After establishing the order of convergence, we apply the mixed finite element method to obtain an algebraic system of equations. Finally, we implement the computational codes in Matlab software and perform the comparison between theory and simulations.
翻译:在本文中,我们考虑的是与p-Baynoric运算器的非线性光束方程式,其中1美元 < p < p\infty$。我们使用变量的变化,将问题转换成一个差异方程式系统,通过应用Lax-Milgram定理和功能分析的经典结果,证明薄弱解决方案的存在、独特性和规律性。我们研究了该系统的离散配方,并在Brouwer定理仪的帮助下,发现问题有一个离散的解决方案。离散解决方案的独特性和稳定性是通过经典方法获得的。在确定趋同顺序后,我们运用混合限定元素方法获取方程式的代数系统。最后,我们在Matlab软件中执行计算代码,并在理论和模拟之间进行比较。