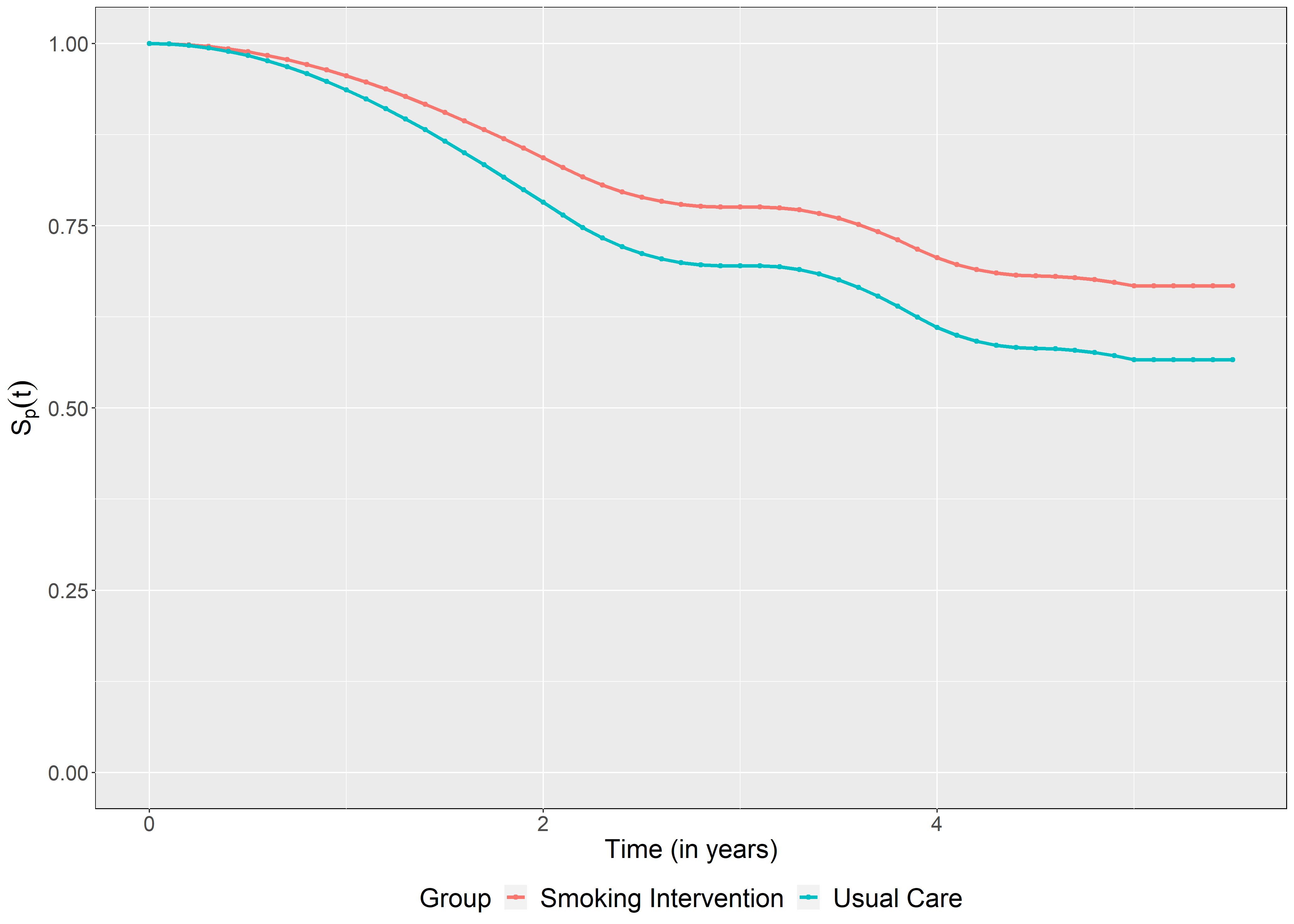
A simple yet effective way of modeling survival data with cure fraction is by considering Box-Cox transformation cure model (BCTM) that unifies mixture and promotion time cure models. In this article, we numerically study the statistical properties of the BCTM when applied to interval censored data. Time-to-events associated with susceptible subjects are modeled through proportional hazards structure that allows for non-homogeneity across subjects, where the baseline hazard function is estimated by distribution-free piecewise linear function with varied degrees of non-parametricity. Due to missing cured statuses for right censored subjects, maximum likelihood estimates of model parameters are obtained by developing an expectation-maximization (EM) algorithm. Under the EM framework, the conditional expectation of the complete data log-likelihood function is maximized by considering all parameters (including the Box-Cox transformation parameter $\alpha$) simultaneously, in contrast to conventional profile-likelihood technique of estimating $\alpha$. The robustness and accuracy of the model and estimation method are established through a detailed simulation study under various parameter settings, and an analysis of real-life data obtained from a smoking cessation study.
翻译:暂无翻译