High-order entropy stable discontinuous Galerkin methods for the shallow water equations: curved triangular meshes and GPU acceleration

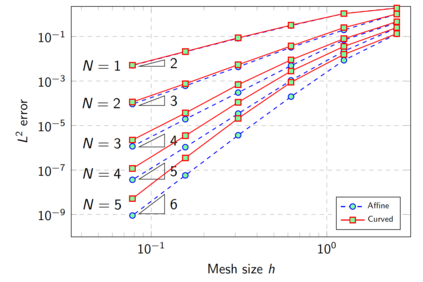
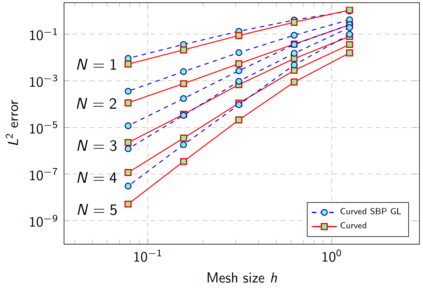
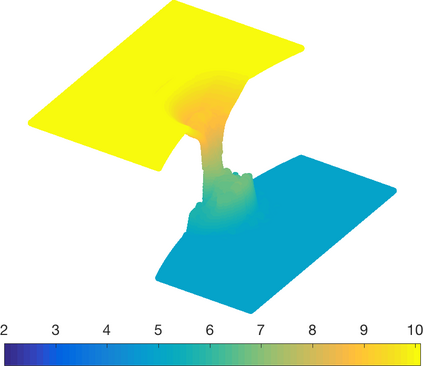
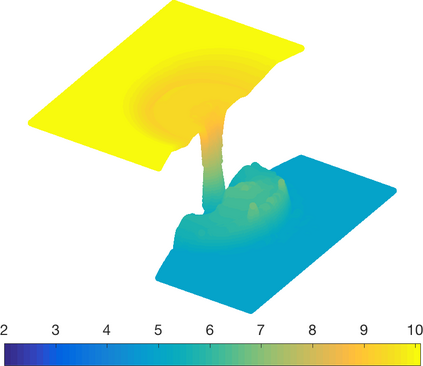
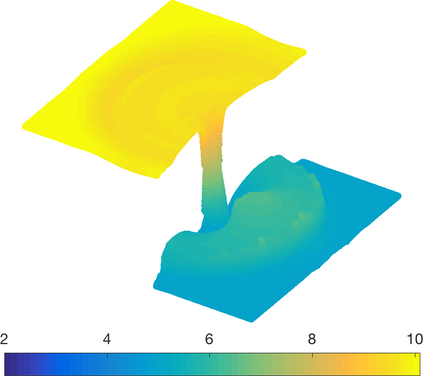
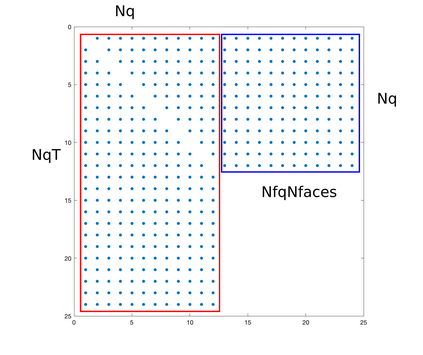
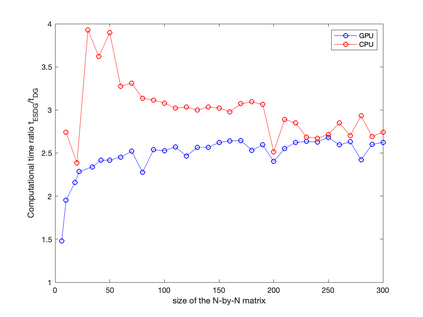
We present a high-order entropy stable discontinuous Galerkin (ESDG) method for the two dimensional shallow water equations (SWE) on curved triangular meshes. The presented scheme preserves a semi-discrete entropy inequality and remains well-balanced for continuous bathymetry profiles. We provide numerical experiments which confirm the high-order accuracy and theoretical properties of the scheme, and compare the presented scheme to an entropy stable scheme based on simplicial summation-by-parts (SBP) finite difference operators. Finally, we report the computational performance of an implementation on Graphics Processing Units (GPUs) and provide comparisons to existing GPU-accelerated implementations of high-order DG methods on quadrilateral meshes.