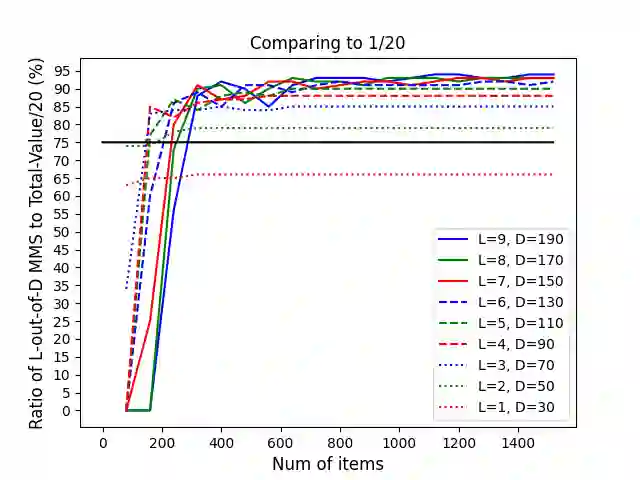
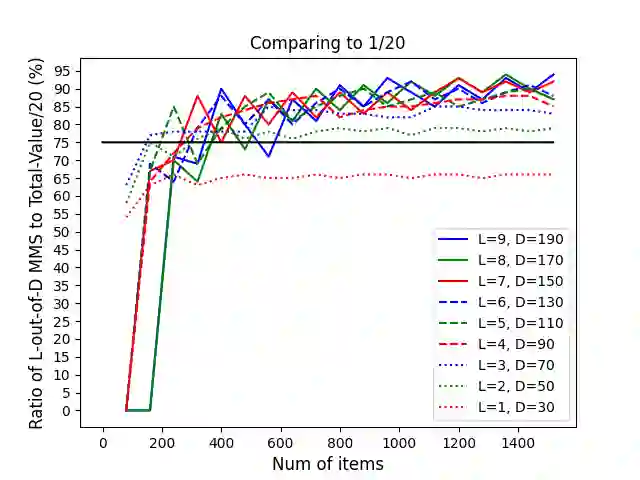
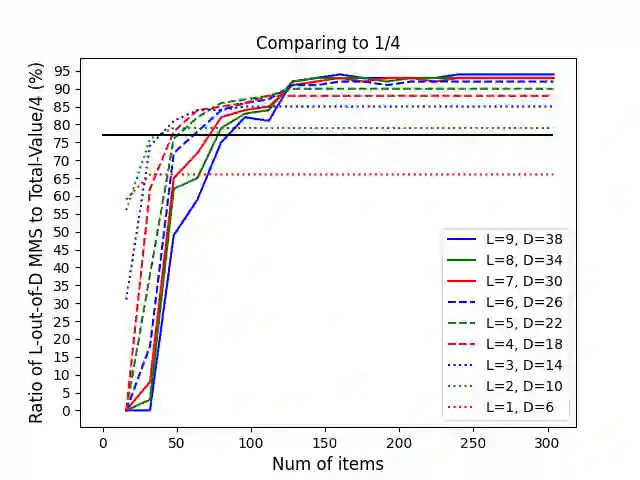
In fair division of indivisible goods, l-out-of-d maximin share (MMS) is the value that an agent can guarantee by partitioning the goods into d bundles and choosing the l least preferred bundles. Most existing works aim to guarantee to all agents a constant fraction of their one-out-of-n MMS. But this guarantee is sensitive to small perturbation in agents' cardinal valuations. We consider a more robust approximation notion, which depends only on the agents' ordinal rankings of bundles. We prove the existence of l-out-of-(l+1/2)n MMS allocations of goods for any integer l >= 1, and develop a polynomial-time algorithm that achieves this guarantee when l = 1.
翻译:在对不可分割货物的公平划分中,I-Out-d最大份额(MMS)是代理人通过将货物分成d捆包和选择最不受欢迎的捆包来保证的价值。大多数现有工作都旨在保证所有代理人的一次性MMS的固定部分。但这一保证对代理人基本价值的小规模扰动十分敏感。我们考虑一种更可靠的近似概念,它只取决于代理人对捆包的定级。我们证明存在任何整数l+1的(l+1/2)n MMS分配货物的情况,并发展一种在l=1时实现这一保证的多元时间算法。