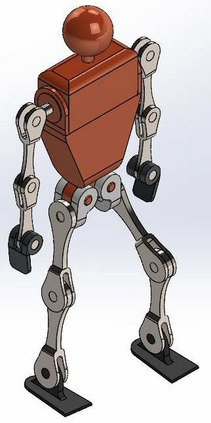
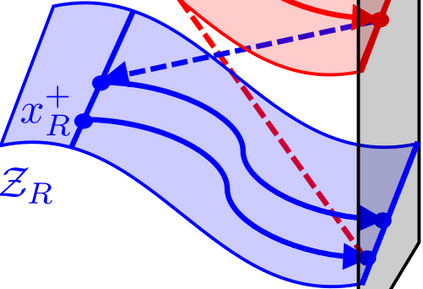
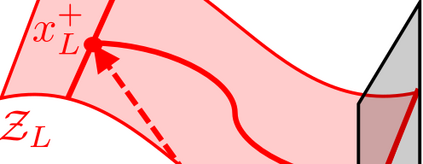
This paper presents a modular approach to motion planning with provable stability guarantees for robots that move through changing environments via periodic locomotion behaviors. We focus on dynamic walkers as a paradigm for such systems, although the tools developed in this paper can be used to support general compositional approaches to robot motion planning with Dynamic Movement Primitives (DMPs). Our approach ensures a priori that the suggested plan can be stably executed. This is achieved by formulating the planning process as a Switching System with Multiple Equilibria (SSME) and proving that the system's evolution remains within explicitly characterized trapping regions in the state space under suitable constraints on the frequency of switching among the DMPs. These conditions effectively encapsulate the low-level stability limitations in a form that can be easily communicated to the planner to guarantee that the suggested plan is compatible with the robot's dynamics. Furthermore, we show how the available primitives can be safely composed online in a receding horizon manner to enable the robot to react to moving obstacles. The proposed framework is applied on 3D bipedal walking models under common modeling assumptions, and offers a modular approach towards stably integrating readily available low-level locomotion control and high-level planning methods.
翻译:本文提出了一种模块化的动态步态规划方法,旨在实现机器人通过周期性的运动行为在变化的环境中移动并具有可证明的稳定性保证。我们以动态步行者作为这种系统的范例,虽然本文开发的工具可以用于支持将动态运动原语(DMP)作为机器人运动规划的一般组合方法。我们的方法在规划过程中保证了规划的成功执行。这是通过将规划过程表述为具有多个平衡点的切换系统(SSME)来实现的,并证明在DMP之间切换的适当约束下,系统的演化将保持在状态空间中的明确字符化陷阱区域中。这些条件有效地封装了形式,可以轻松地向规划者通信,以确保提议的规划与机器人的动态兼容。此外,我们展示了可用于在滑动环境中反应的计划如何在向后的地平线方式下安全地在线进行组合。所提出的框架应用于常见的建模假设下的3D双足行走模型,并提供用于稳定地集成可获得的低级运动控制和高级规划方法的模块化方法。