Quantum Advantage for All

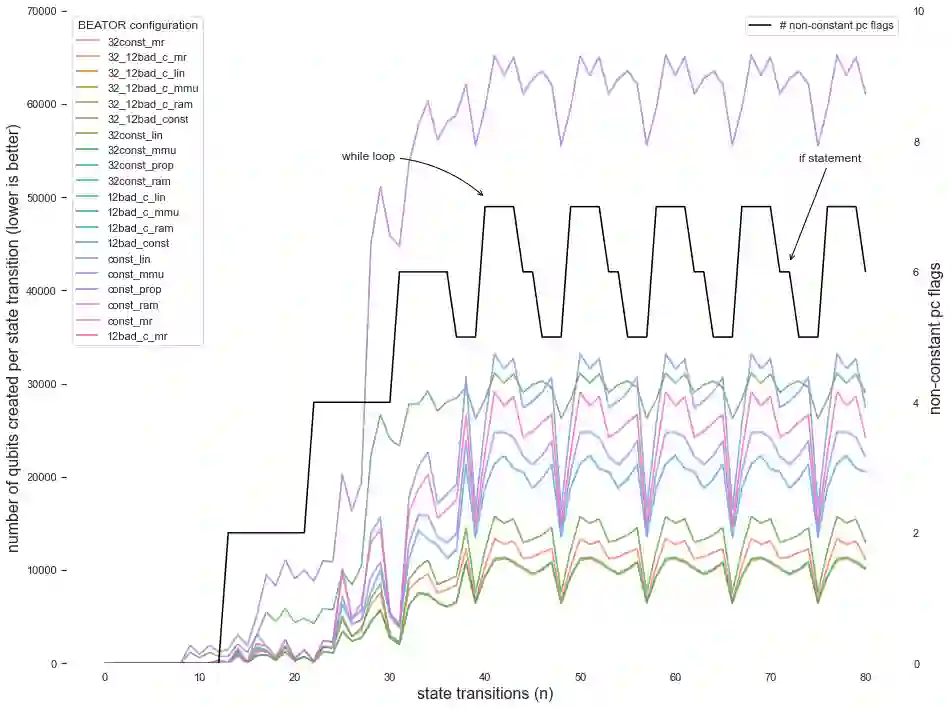
We show how to translate a subset of RISC-V machine code compiled from a subset of C to quadratic unconstrained binary optimization (QUBO) models that can be solved by a quantum annealing machine: given a bound $n$, there is input $I$ to a program $P$ such that $P$ runs into a given program state $E$ executing no more than $n$ machine instructions if and only if the QUBO model of $P$ for $n$ evaluates to 0 on $I$. Thus, with more qubits on the machine than variables in the QUBO model, quantum annealing the model reaches 0 (ground) energy in constant time with high probability on some input $I$ that is part of the ground state if and only if $P$ runs into $E$ on $I$ executing no more than $n$ instructions. Translation takes $\mathcal{O}(n^2)$ time effectively turning a quantum annealer into a polynomial-time symbolic execution engine and bounded model checker, eliminating their path and state explosion problems. Here, we take advantage of the fact that any machine instruction may only increase the size of the program state by a constant amount of bits. Translation time comes down from $\mathcal{O}(n^2)$ to $\mathcal{O}(n\cdot|P|)$ if memory consumption of $P$ is bounded by a constant, establishing a linear (quadratic) upper bound on quantum space, in number of qubits on a quantum annealer, in terms of algorithmic time (space) in classical computing, implying $NP\subseteq BQP$. Our prototypical open-source toolchain translates machine code that runs on real RISC-V hardware to models that can be solved by real quantum annealing hardware, as shown in our experiments.