An Empirical Review of Optimization Techniques for Quantum Variational Circuits

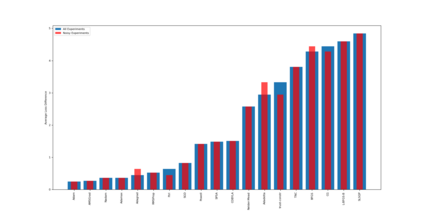
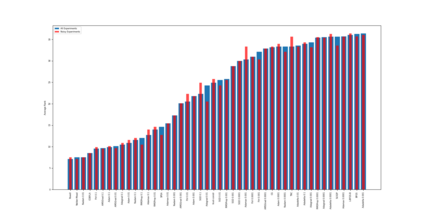
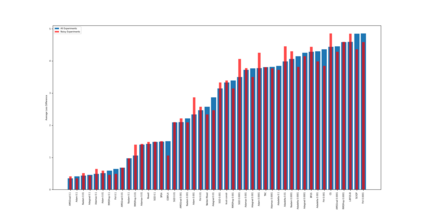
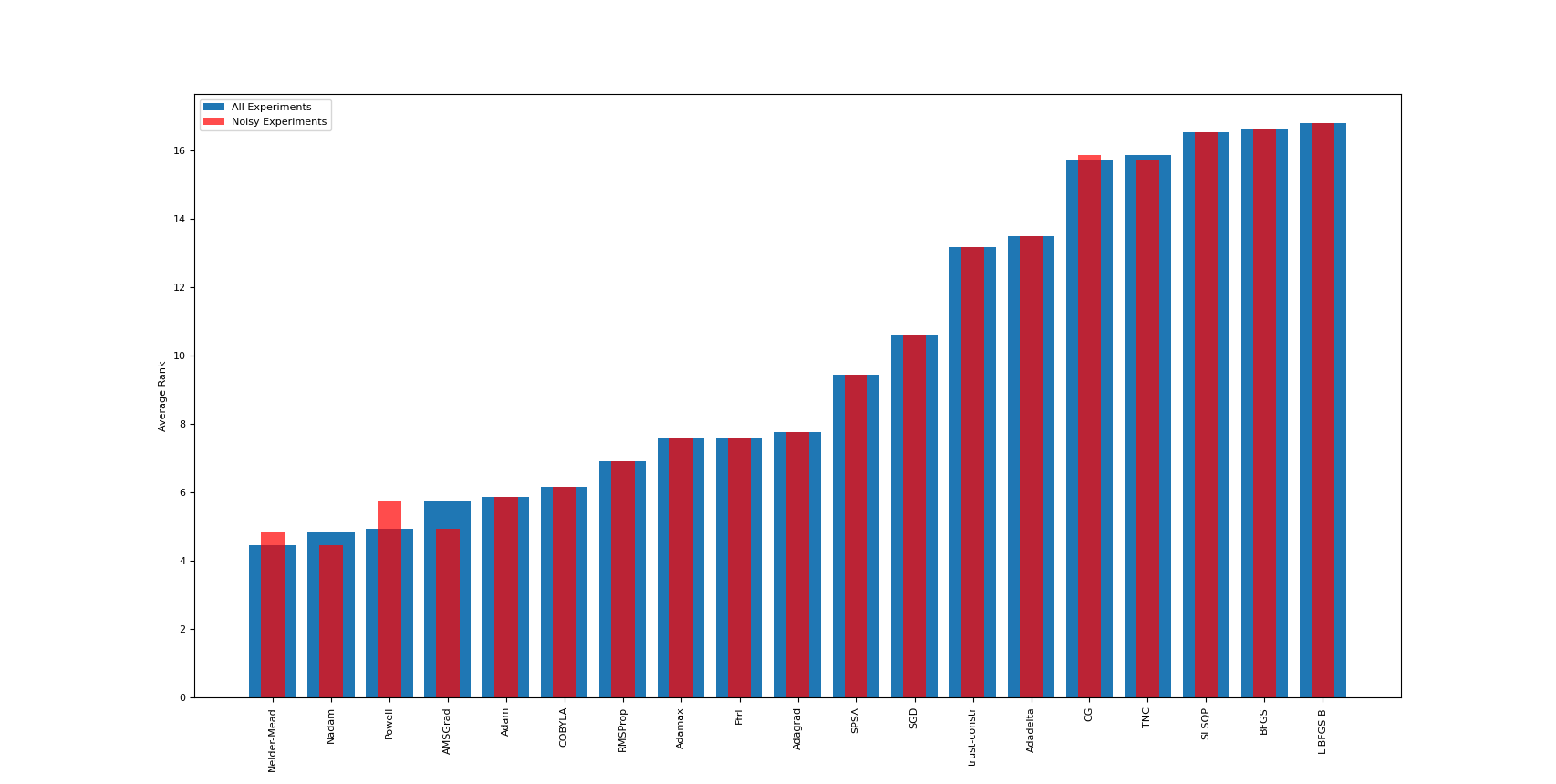
Quantum Variational Circuits (QVCs) are often claimed as one of the most potent uses of both near term and long term quantum hardware. The standard approaches to optimizing these circuits rely on a classical system to compute the new parameters at every optimization step. However, this process can be extremely challenging both in terms of navigating the exponentially scaling complex Hilbert space, barren plateaus, and the noise present in all foreseeable quantum hardware. Although a variety of optimization algorithms are employed in practice, there is often a lack of theoretical or empirical motivations for this choice. To this end we empirically evaluate the potential of many common gradient and gradient free optimizers on a variety of optimization tasks. These tasks include both classical and quantum data based optimization routines. Our evaluations were conducted in both noise free and noisy simulations. The large number of problems and optimizers yields strong empirical guidance for choosing optimizers for QVCs that is currently lacking.