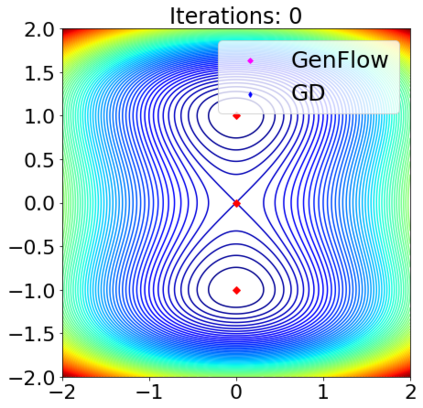
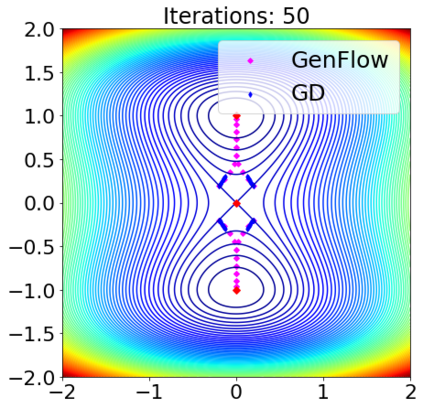
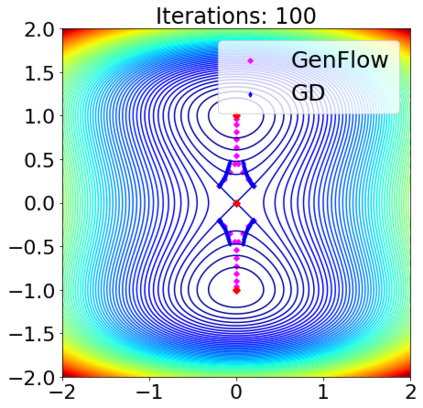
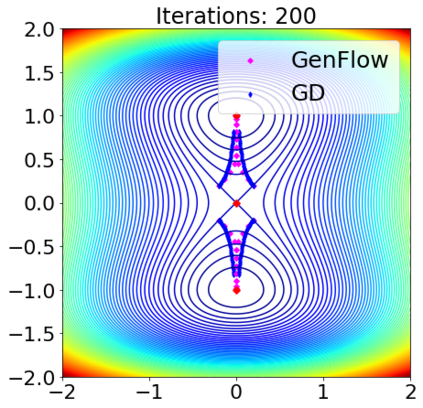
Gradient-based first-order convex optimization algorithms find widespread applicability in a variety of domains, including machine learning tasks. Motivated by the recent advances in fixed-time stability theory of continuous-time dynamical systems, we introduce a generalized framework for designing accelerated optimization algorithms with strongest convergence guarantees that further extend to a subclass of non-convex functions. In particular, we introduce the \emph{GenFlow} algorithm and its momentum variant that provably converge to the optimal solution of objective functions satisfying the Polyak-{\L}ojasiewicz (PL) inequality, in a fixed-time. Moreover for functions that admit non-degenerate saddle-points, we show that for the proposed GenFlow algorithm, the time required to evade these saddle-points is bounded uniformly for all initial conditions. Finally, for strongly convex-strongly concave minimax problems whose optimal solution is a saddle point, a similar scheme is shown to arrive at the optimal solution again in a fixed-time. The superior convergence properties of our algorithm are validated experimentally on a variety of benchmark datasets.
翻译:基于梯级的一级共振优化算法在包括机器学习任务在内的各个领域都具有广泛适用性。在连续时间动态系统固定时间稳定理论最近取得进展的推动下,我们引入了一个通用框架,设计加速优化算法,提供最有力的趋同保证,进一步扩展至非 convex 功能的子类。特别是,我们引入了 emph{GenFlow} 算法及其动因变量,这种算法在固定时间可以明显地接近于满足Polyak-L}ojasiewicz(PL)不平等的客观功能的最佳解决方案。此外,对于接受非降解性马鞍点的功能,我们显示,对于拟议的GenFlow 算法,在所有初始条件下,绕过这些马鞍点所需的时间是统一的。最后,对于最优化的解决方案是支撑点的强烈的 convex-strong-concave 迷轴问题,一个类似的方案显示在固定时间再次达到最佳解决方案。对于各种基准数据集,我们算法的高级趋同特性是经过实验性验证的。