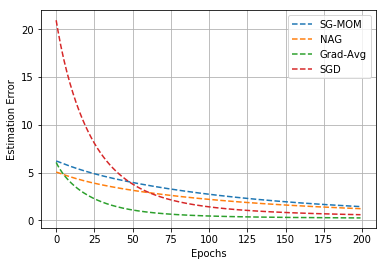
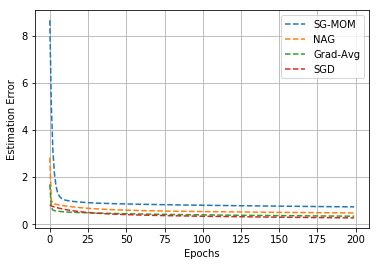
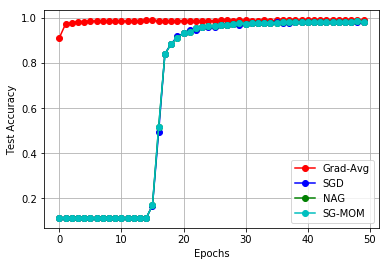
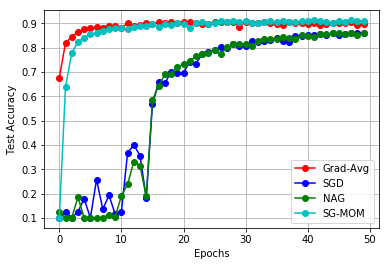
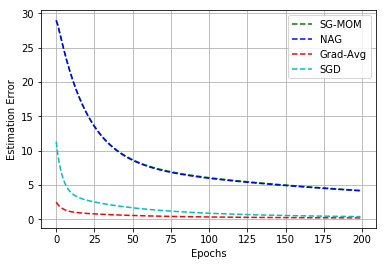
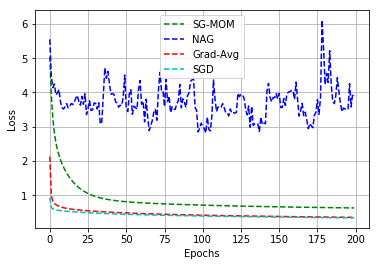
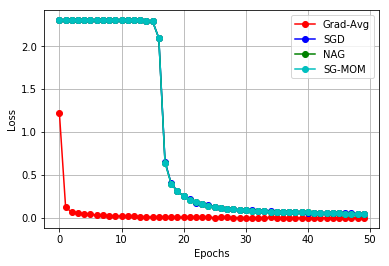
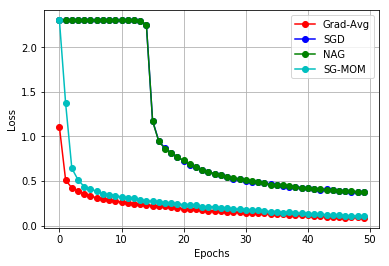
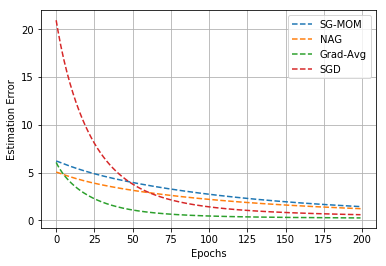
In this work, we study an optimizer, Grad-Avg to optimize error functions. We establish the convergence of the sequence of iterates of Grad-Avg mathematically to a minimizer (under boundedness assumption). We apply Grad-Avg along with some of the popular optimizers on regression as well as classification tasks. In regression tasks, it is observed that the behaviour of Grad-Avg is almost identical with Stochastic Gradient Descent (SGD). We present a mathematical justification of this fact. In case of classification tasks, it is observed that the performance of Grad-Avg can be enhanced by suitably scaling the parameters. Experimental results demonstrate that Grad-Avg converges faster than the other state-of-the-art optimizers for the classification task on two benchmark datasets.
翻译:在这项工作中,我们研究一个优化器, Grad-Avg 优化错误函数。 我们从数学角度将 Grad- Avg 的迭代序列与最小化器相融合( 受约束假设 ) 。 我们将 Grad- Avg 和一些流行的优化器一起应用到回归和分类任务上。 在回归任务中, 观察到 Grad- Avg 的行为与 Stochatic 梯子源( SGD ) 几乎完全相同 。 我们从数学角度解释了这一事实。 在分类任务中, 观察到 Grad- Avg 的性能可以通过适当缩放参数来提高。 实验结果显示, Grad- Avg 与其他最先进的优化器在两个基准数据集的分类任务上趋近。