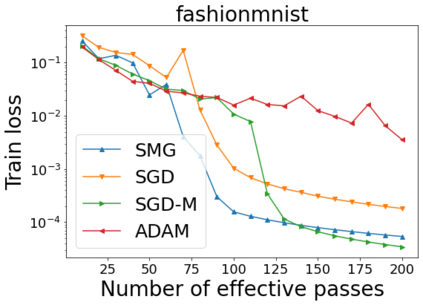
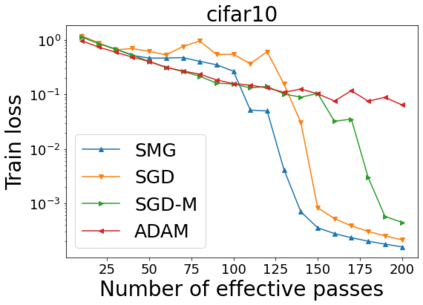
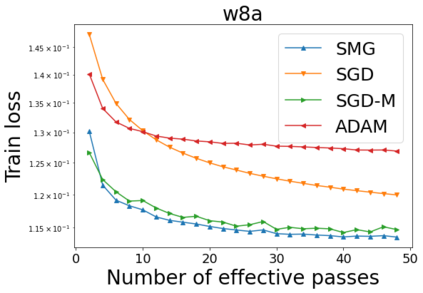
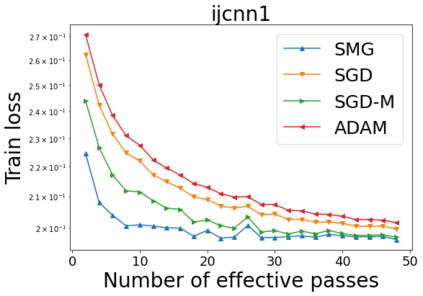
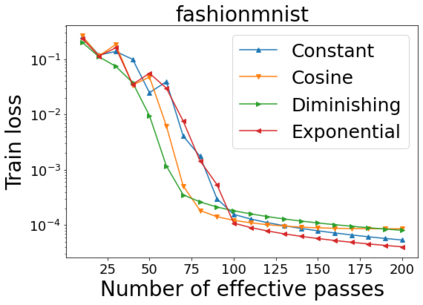
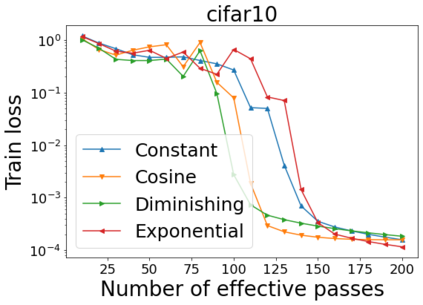
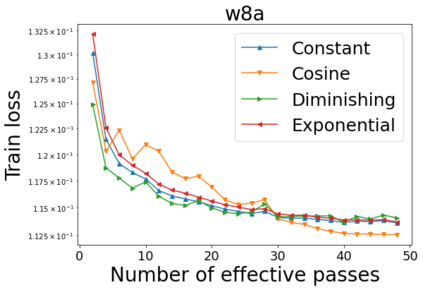
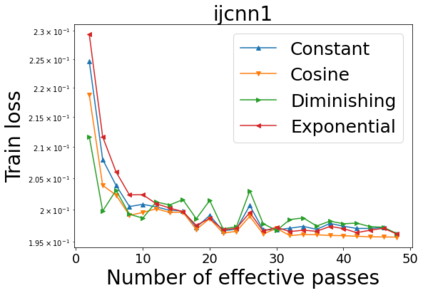
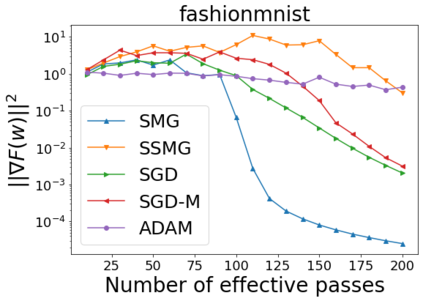
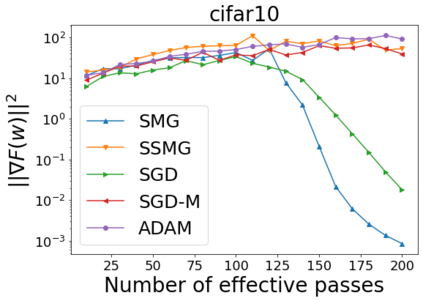
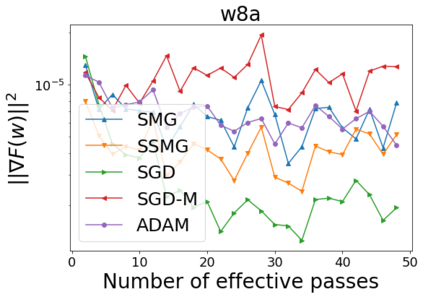
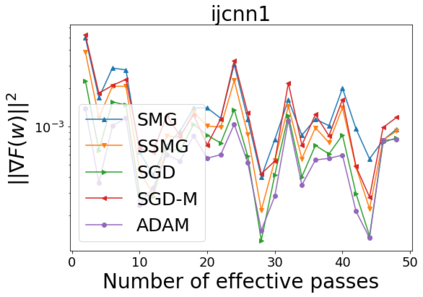
We combine two advanced ideas widely used in optimization for machine learning: shuffling strategy and momentum technique to develop a novel shuffling gradient-based method with momentum to approximate a stationary point of non-convex finite-sum minimization problems. While our method is inspired by momentum techniques, its update is fundamentally different from existing momentum-based methods. We establish that our algorithm achieves a state-of-the-art convergence rate for both constant and diminishing learning rates for any shuffling strategy under standard assumptions (i.e., L-smoothness and bounded variance). In particular, if a randomized reshuffling strategy is used, we can further improve our convergence rate by a fraction of the data size. When the shuffling strategy is fixed, we develop another new algorithm that is similar to existing momentum methods. This algorithm covers the single-shuffling and incremental gradient schemes as special cases. We prove the same convergence rate of this algorithm under the L-smoothness and bounded gradient assumptions. We demonstrate our algorithms via numerical simulations on standard datasets and compare them with existing shuffling methods. Our tests have shown encouraging performance of the new algorithms.
翻译:我们结合了在优化机器学习中广泛使用的两个先进想法:调整战略和动力技术,以开发一种全新的以梯度为基础的洗涤方法,并形成一种势头,以接近非螺旋有限和最小化问题的固定点。虽然我们的方法受动力技术的启发,但其更新与现有的动力方法有根本的不同。我们确定,我们的算法在标准假设(即,L-moothity和受约束的梯度假设)下,在任何洗涤战略的常数和不断减少的学习率方面都达到了一种最先进的趋同率。特别是,如果采用随机调整战略,我们可以通过数据大小的一小部分来进一步提高我们的趋同率。当打动战略固定下来时,我们将开发与现有动力方法类似的另一种新的算法。这一算法包括单打动和递增梯度计划的特殊情况。我们证明,在L-moooth和受约束的梯度假设下,这种算法的趋同速度。我们通过对标准数据集进行数字模拟来展示我们的算法,并将它们与现有的抖法进行比较。我们的测试显示,新的算法表现了令人鼓舞的。