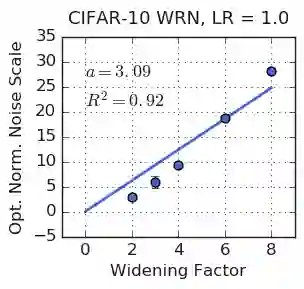
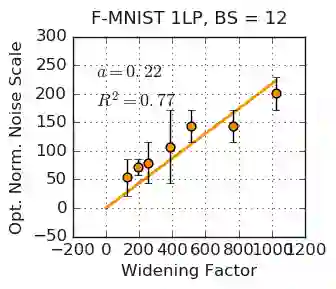
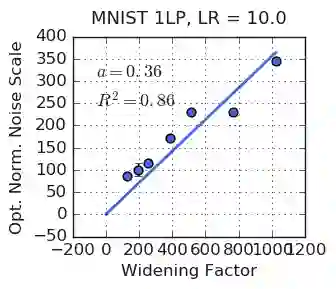
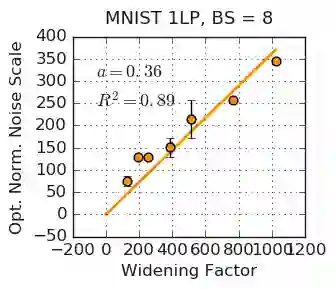
We investigate how the final parameters found by stochastic gradient descent are influenced by over-parameterization. We generate families of models by increasing the number of channels in a base network, and then perform a large hyper-parameter search to study how the test error depends on learning rate, batch size, and network width. We find that the optimal SGD hyper-parameters are determined by a "normalized noise scale," which is a function of the batch size, learning rate, and initialization conditions. In the absence of batch normalization, the optimal normalized noise scale is directly proportional to width. Wider networks, with their higher optimal noise scale, also achieve higher test accuracy. These observations hold for MLPs, ConvNets, and ResNets, and for two different parameterization schemes ("Standard" and "NTK"). We observe a similar trend with batch normalization for ResNets. Surprisingly, since the largest stable learning rate is bounded, the largest batch size consistent with the optimal normalized noise scale decreases as the width increases.
翻译:我们调查了由悬浮梯度梯度下降发现的最后参数是如何受过度参数影响。 我们通过增加基网的频道数量来生成模型群, 然后进行大型超参数搜索, 研究测试错误如何取决于学习率、 批量大小和网络宽度。 我们发现, 最佳 SGD 超参数是由“ 正常噪声比例尺” 所决定的, 这是批量规模、 学习率和初始化条件的函数。 在没有批量正常化的情况下, 最佳的标准化噪声比例尺与宽度直接成比例。 大的网络, 其最佳噪声比例更高, 也实现了更高的测试精确度。 这些观测结果为 MLPs、 ConvNets 和ResNets 以及 两种不同的参数化计划( “ Standard” 和 “ NTK ” ) 所维持。 我们观察到的是, 最稳定的学习率是结合最大, 随着宽度的增加, 最大与最佳标准化噪声比例下降, 最大的批量大小与最佳的标准化比例相近。