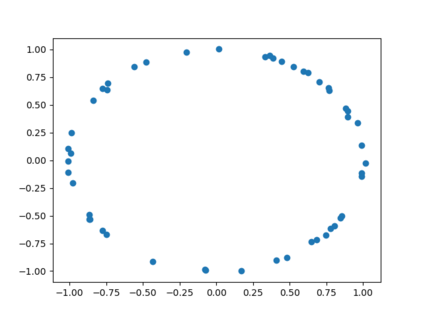
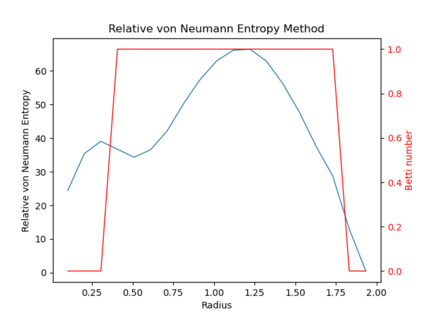
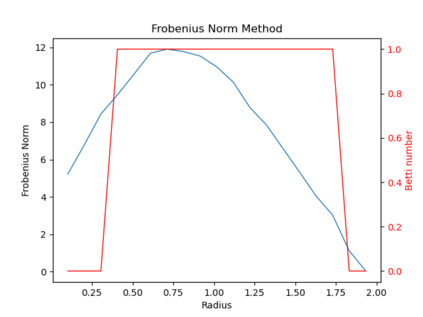
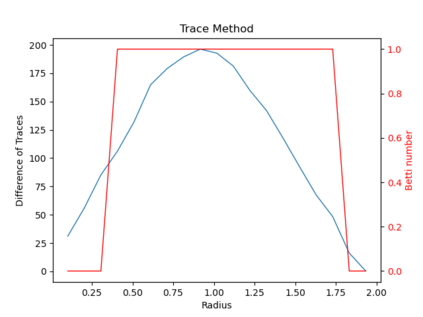
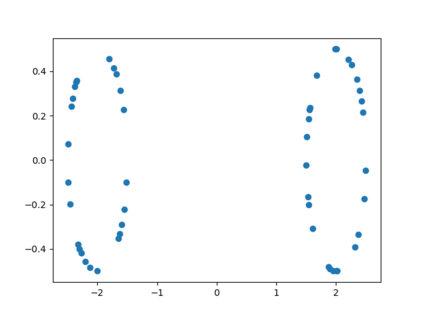
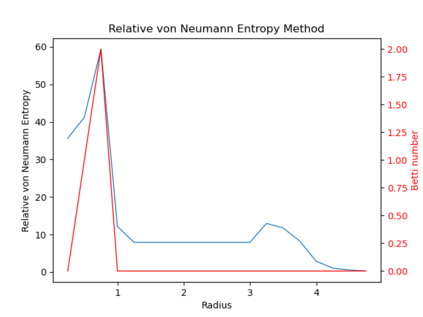
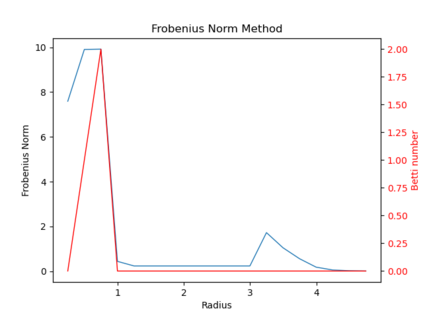
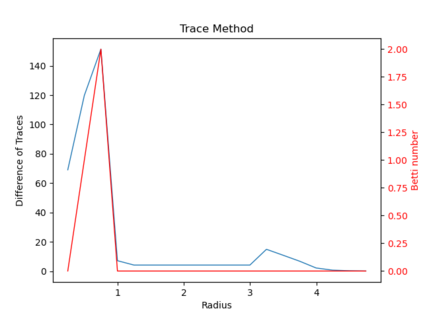
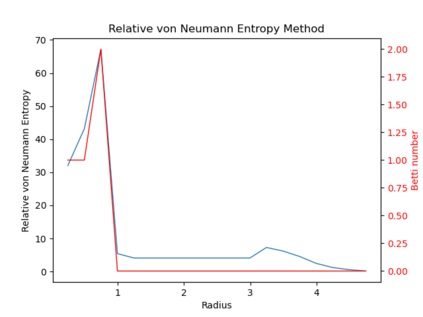
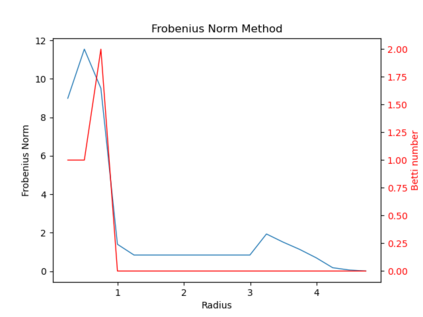
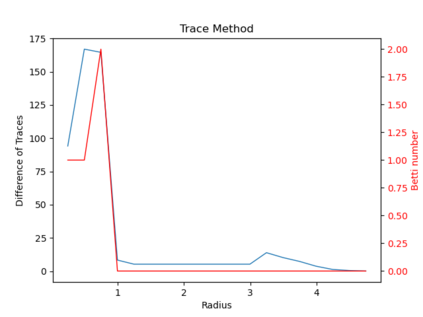
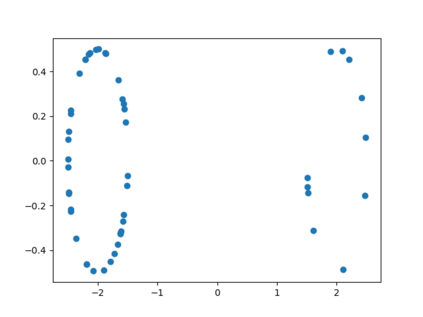
We propose three completely data-driven methods for estimating the real cohomology groups $H^k (X ; \mathbb{R})$ of a compact metric-measure space $(X, d_X, \mu_X)$ embedded in a metric-measure space $(Y,d_Y,\mu_Y)$, given a finite set of points $S$ sampled from a uniform distrbution $\mu_X$ on $X$, possibly corrupted with noise from $Y$. We present the results of several computational experiments in the case that $X$ is embedded in $\mathbb{R}^n$, where two of the three algorithms performed well.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
13+阅读 · 2023年11月2日
Arxiv
22+阅读 · 2022年9月29日
Arxiv
17+阅读 · 2022年5月10日
Arxiv
12+阅读 · 2020年12月14日
Arxiv
34+阅读 · 2019年10月24日