An augmented mixed FEM for the convective Brinkman-Forchheimer problem: a priori and a posteriori error analysis

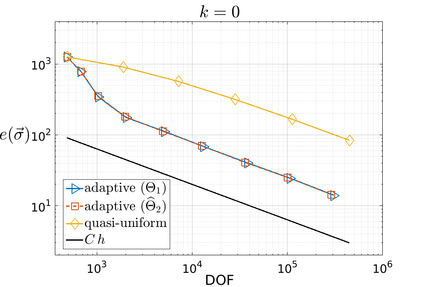
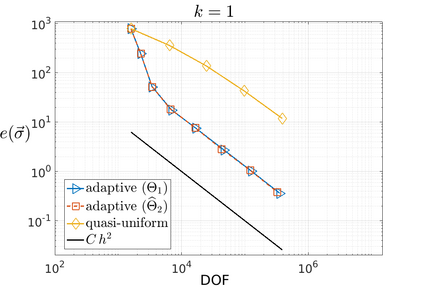
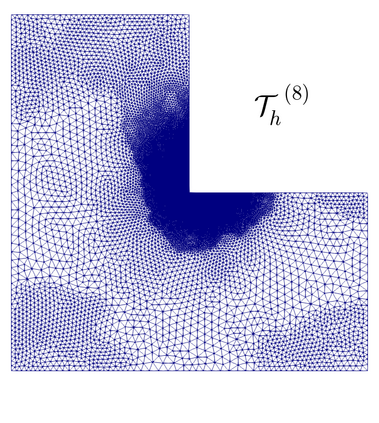
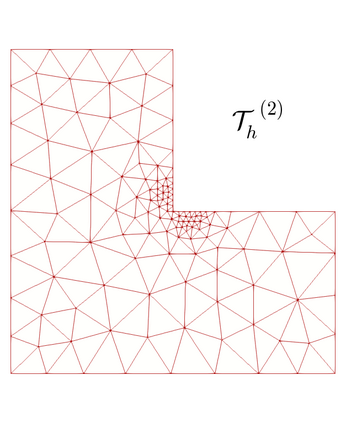
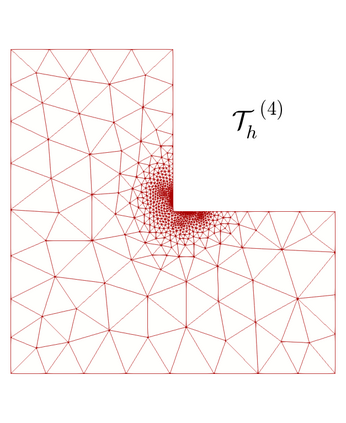
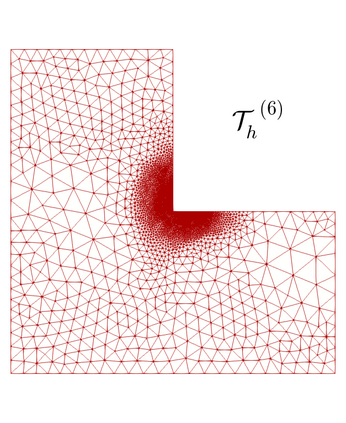
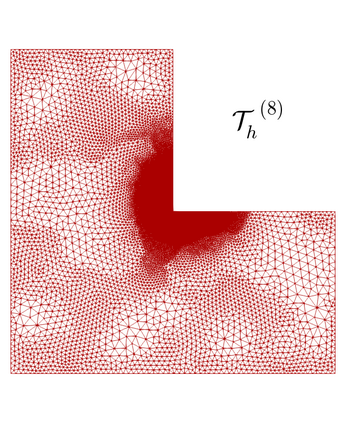
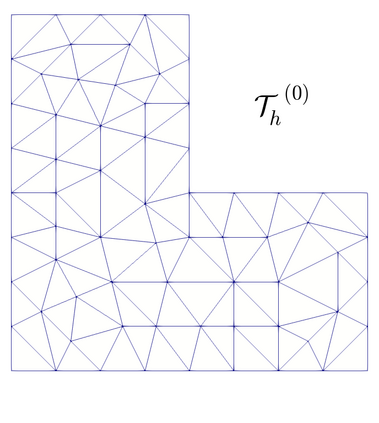
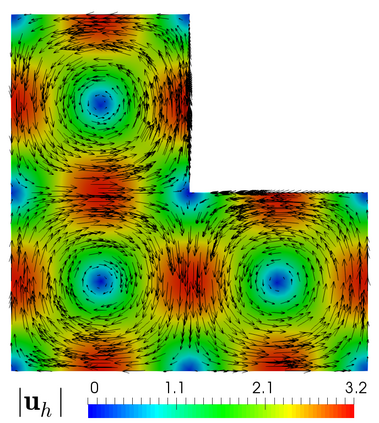
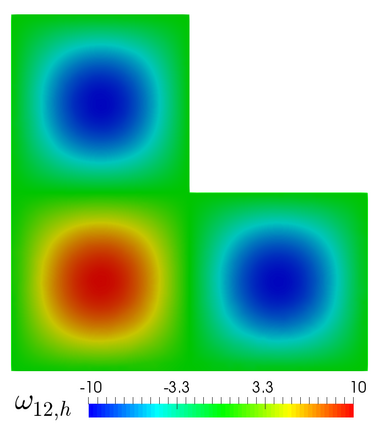
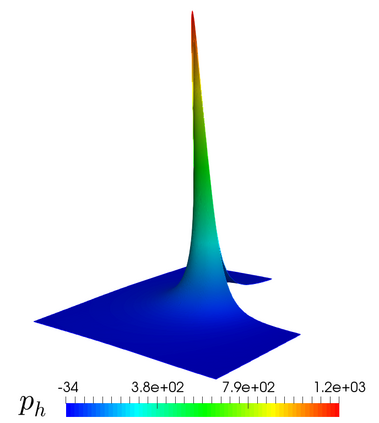
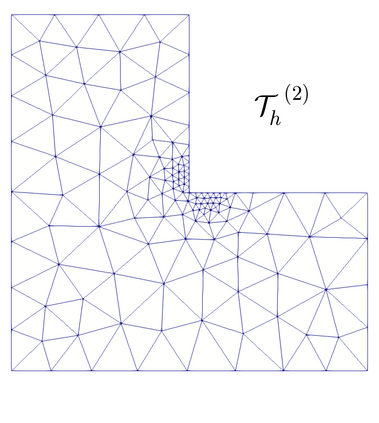
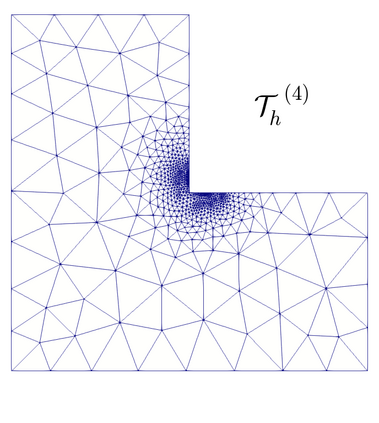
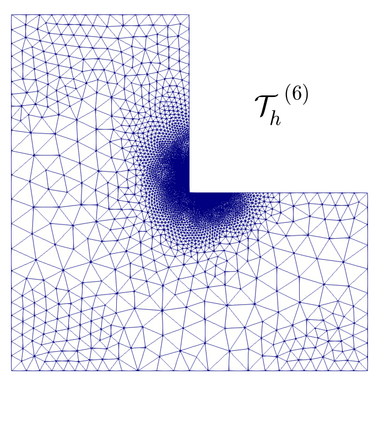
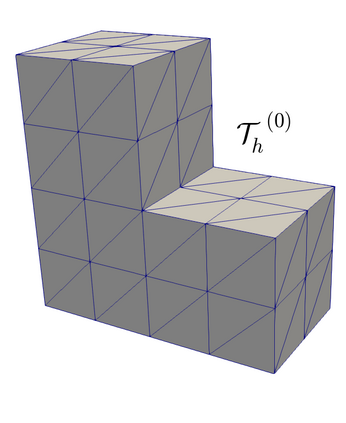
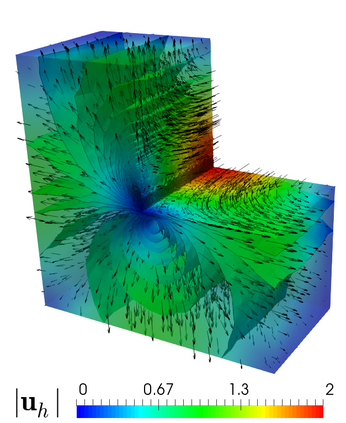
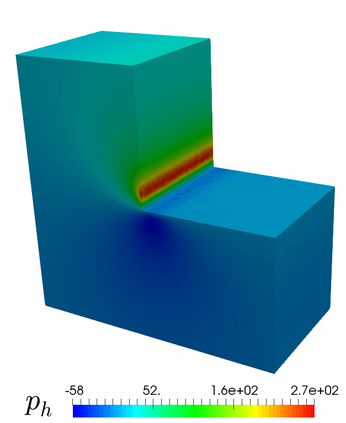
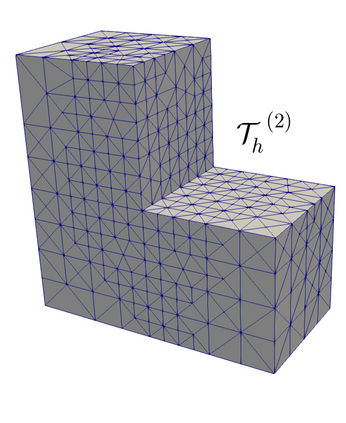
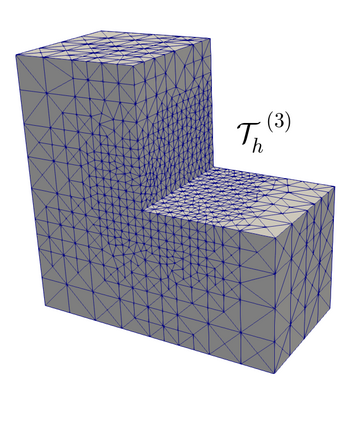
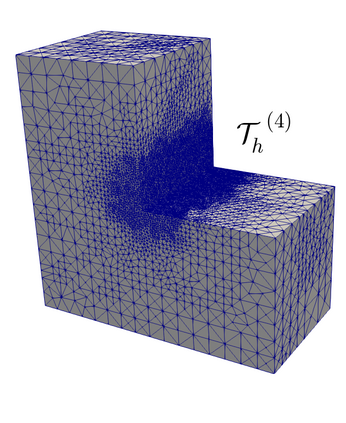
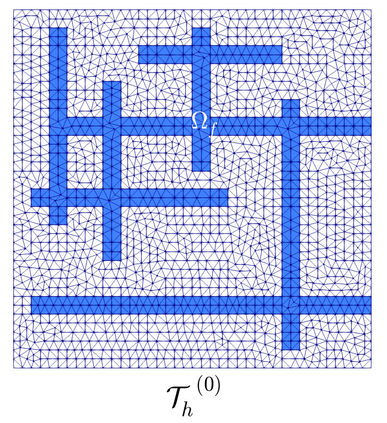
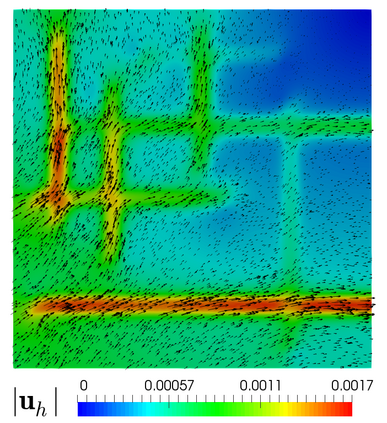
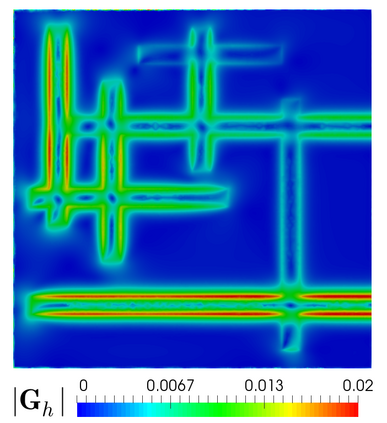
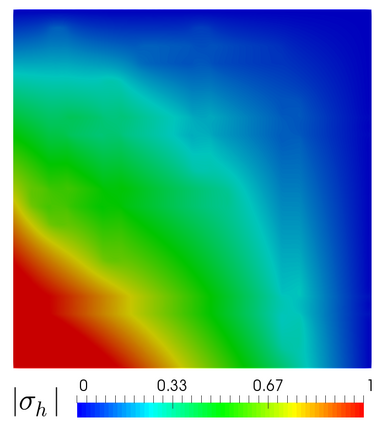
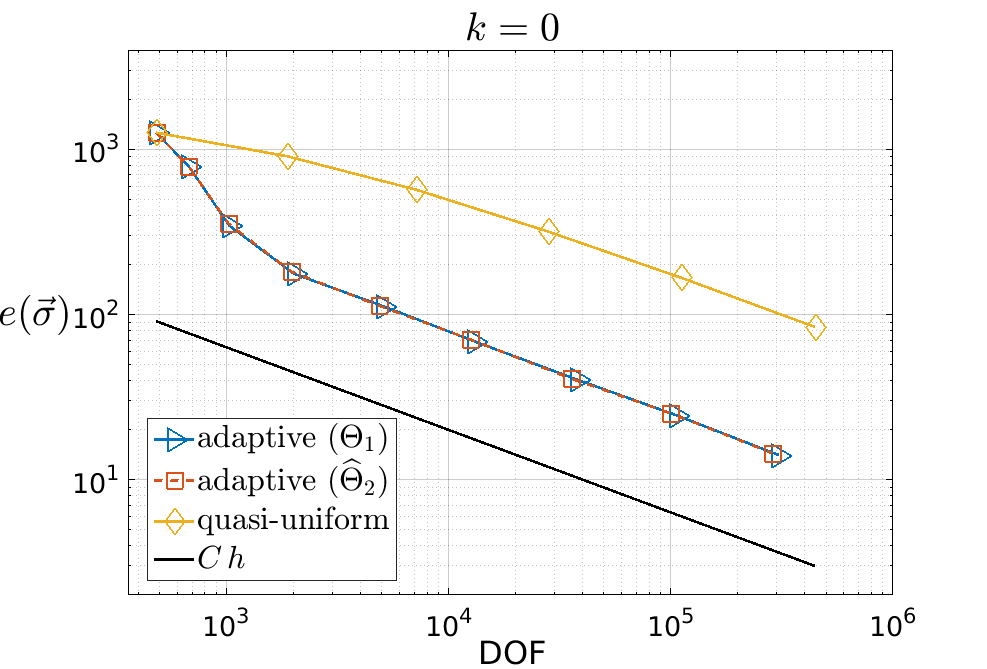
We propose and analyze an augmented mixed finite element method for the pseudostress-velocity formulation of the stationary convective Brinkman-Forchheimer problem in $\mathrm{R}^d$, $d\in \{2,3\}$. Since the convective and Forchheimer terms forces the velocity to live in a smaller space than usual, we augment the variational formulation with suitable Galerkin type terms. The resulting augmented scheme is written equivalently as a fixed point equation, so that the well-known Schauder and Banach theorems, combined with the Lax-Milgram theorem, allow to prove the unique solvability of the continuous problem. The finite element discretization involves Raviart-Thomas spaces of order $k\geq 0$ for the pseudostress tensor and continuous piecewise polynomials of degree $\le k + 1$ for the velocity. Stability, convergence, and a priori error estimates for the associated Galerkin scheme are obtained. In addition, we derive two reliable and efficient residual-based a posteriori error estimators for this problem on arbitrary polygonal and polyhedral regions. The reliability of the proposed estimators draws mainly upon the uniform ellipticity of the form involved, a suitable assumption on the data, a stable Helmholtz decomposition, and the local approximation properties of the Cl\'ement and Raviart-Thomas operators. In turn, inverse inequalities, the localization technique based on bubble functions, and known results from previous works, are the main tools yielding the efficiency estimate. Finally, some numerical examples illustrating the performance of the mixed finite element method, confirming the theoretical rate of convergence and the properties of the estimators, and showing the behaviour of the associated adaptive algorithms, are reported. In particular, the case of flow through a $2$D porous media with fracture networks is considered.