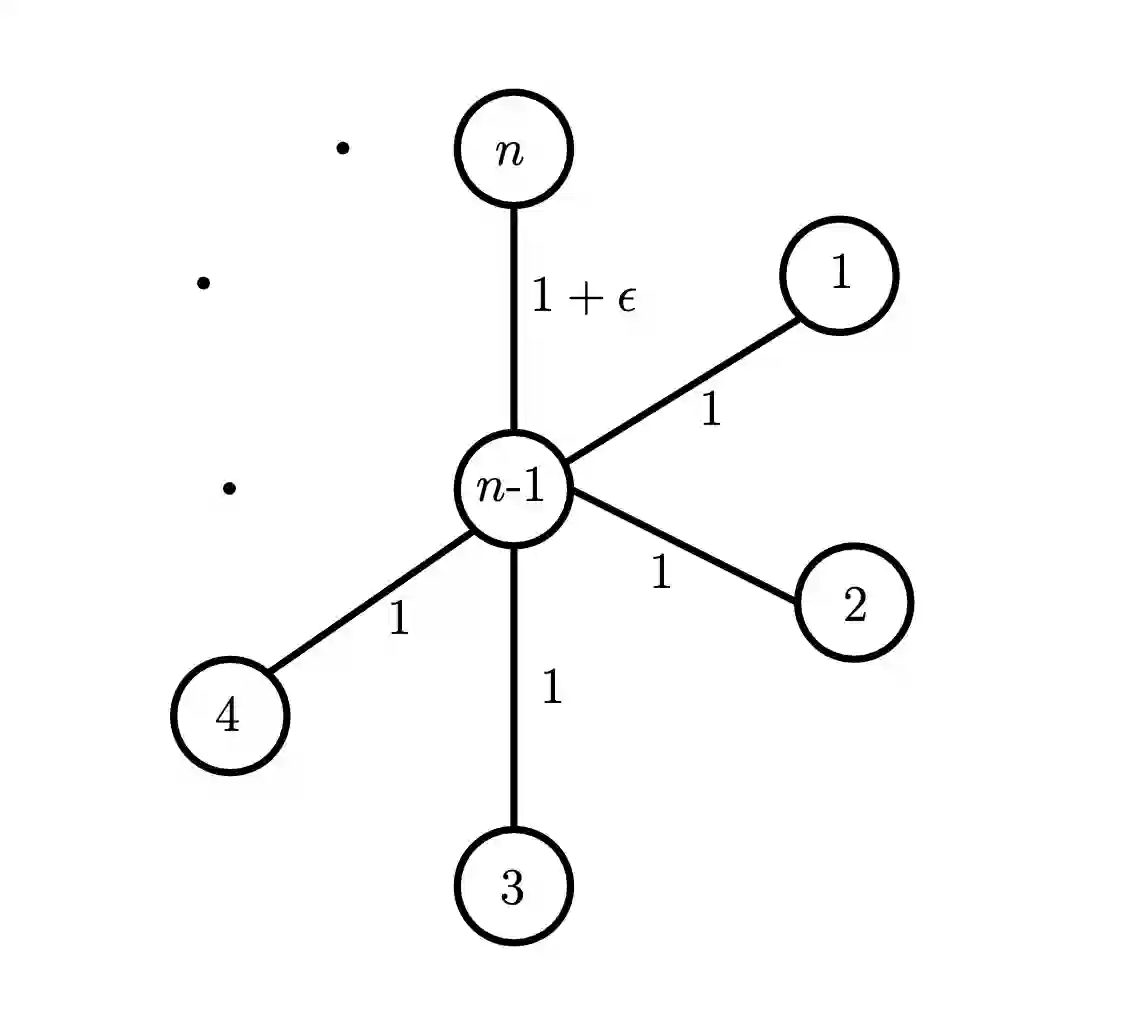
Given a mapping from a set of players to the leaves of a complete binary tree (called a seeding), a knockout tournament is conducted as follows: every round, every two players with a common parent compete against each other, and the winner is promoted to the common parent; then, the leaves are deleted. When only one player remains, it is declared the winner. This is a popular competition format in sports, elections, and decision-making. Over the past decade, it has been studied intensively from both theoretical and practical points of view. Most frequently, the objective is to seed the tournament in a way that "assists" (or even guarantees) some particular player to win the competition. We introduce a new objective, which is very sensible from the perspective of the directors of the competition: maximize the profit or popularity of the tournament. Specifically, we associate a "score" with every possible match, and aim to seed the tournament to maximize the sum of the scores of the matches that take place. We focus on the case where we assume a total order on the players' strengths, and provide a wide spectrum of results on the computational complexity of the problem.
翻译:暂无翻译