From Tensor Network Quantum States to Tensorial Recurrent Neural Networks

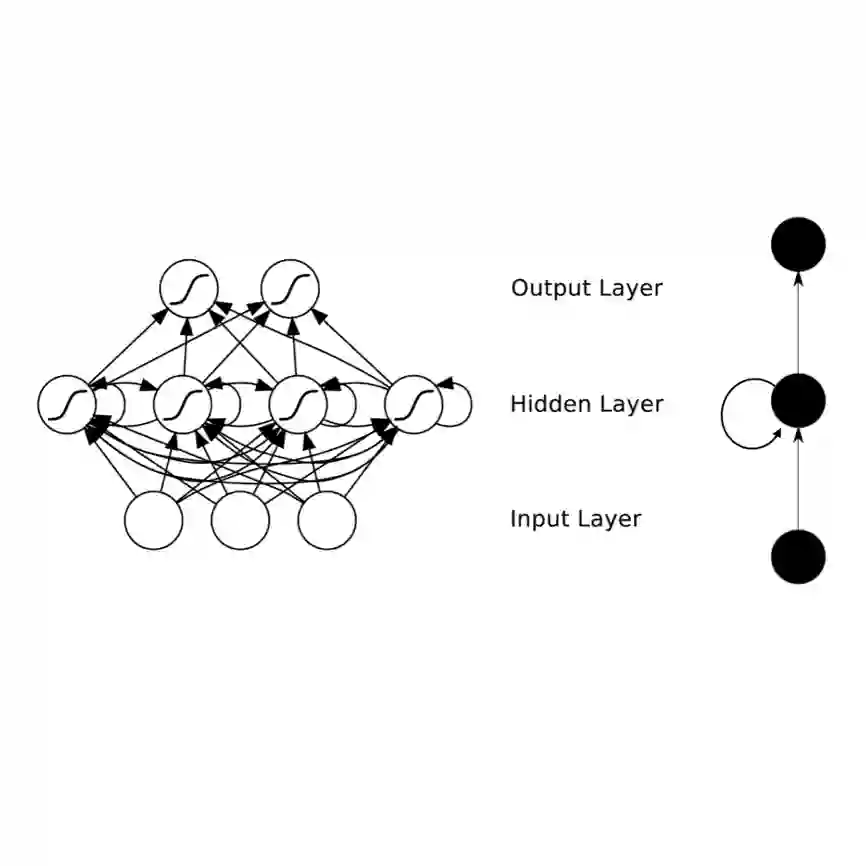
We show that any matrix product state (MPS) can be exactly represented by a recurrent neural network (RNN) with a linear memory update. We generalize this RNN architecture to 2D lattices using a multilinear memory update. It supports perfect sampling and wave function evaluation in polynomial time, and can represent an area law of entanglement entropy. Numerical evidence shows that it can encode the wave function using a bond dimension lower by orders of magnitude when compared to MPS, with an accuracy that can be systematically improved by increasing the bond dimension.