The Quantified Boolean Bayesian Network: Theory and Experiments with a Logical Graphical Model

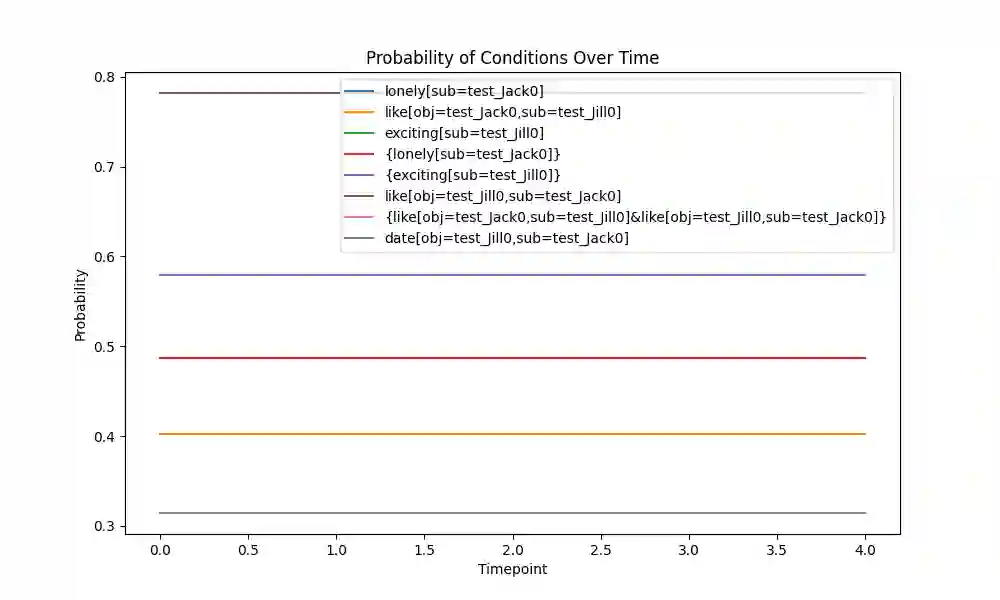
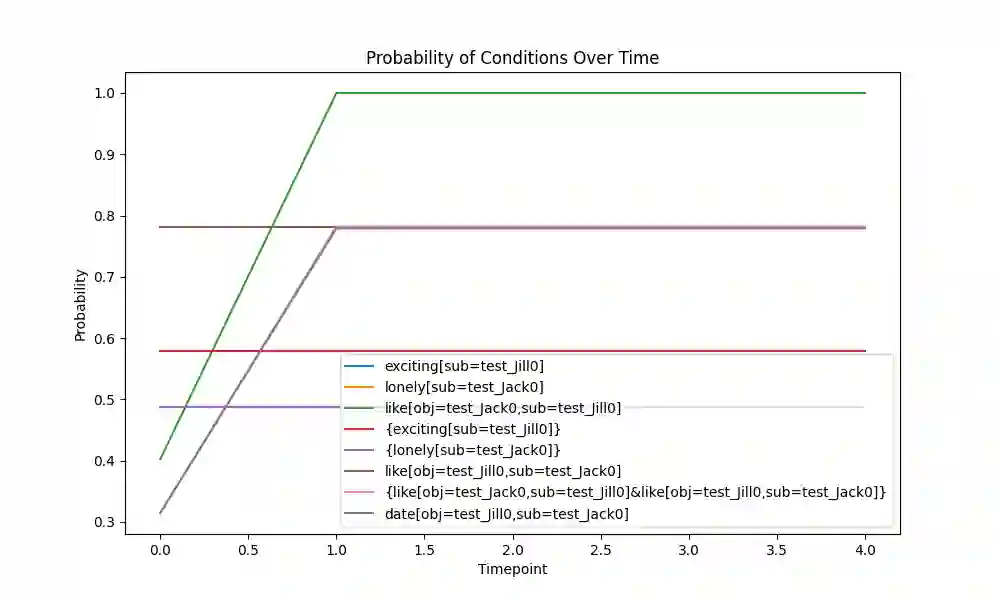
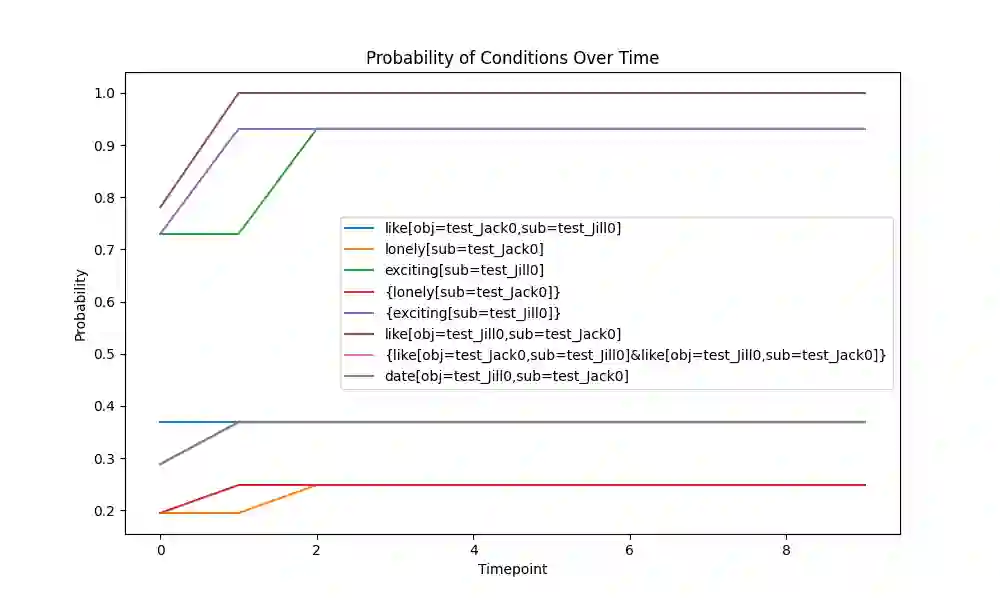
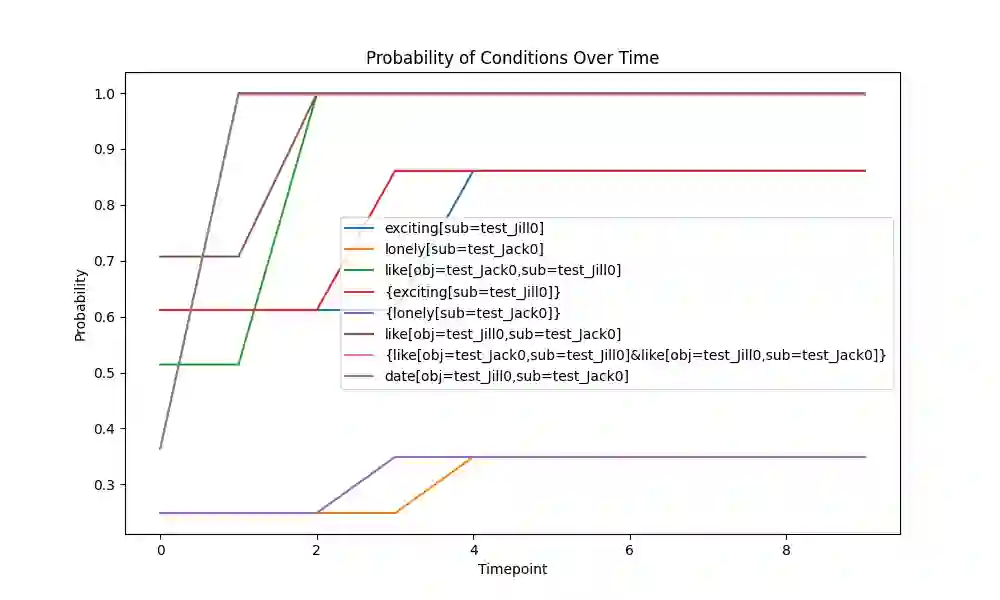
This paper introduces the Quantified Boolean Bayesian Network (QBBN), which provides a unified view of logical and probabilistic reasoning. The QBBN is meant to address a central problem with the Large Language Model (LLM), which has become extremely popular in Information Retrieval, which is that the LLM hallucinates. A Bayesian Network, by construction, cannot hallucinate, because it can only return answers that it can explain. We show how a Bayesian Network over an unbounded number of boolean variables can be configured to represent the logical reasoning underlying human language. We do this by creating a key-value version of the First-Order Calculus, for which we can prove consistency and completeness. We show that the model is trivially trained over fully observed data, but that inference is non-trivial. Exact inference in a Bayesian Network is intractable (i.e. $\Omega(2^N)$ for $N$ variables). For inference, we investigate the use of Loopy Belief Propagation (LBP), which is not guaranteed to converge, but which has been shown to often converge in practice. Our experiments show that LBP indeed does converge very reliably, and our analysis shows that a round of LBP takes time $O(N2^n)$, where $N$ bounds the number of variables considered, and $n$ bounds the number of incoming connections to any factor, and further improvements may be possible. Our network is specifically designed to alternate between AND and OR gates in a Boolean Algebra, which connects more closely to logical reasoning, allowing a completeness proof for an expanded version of our network, and also allows inference to follow specific but adequate pathways, that turn out to be fast.