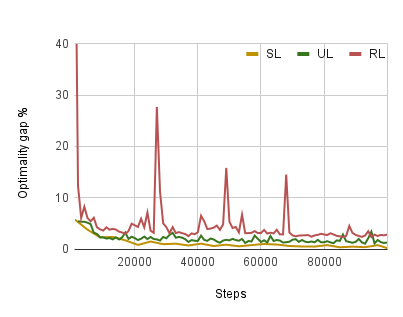
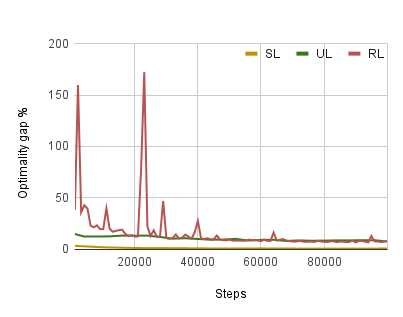
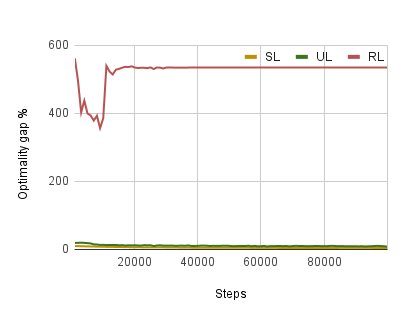
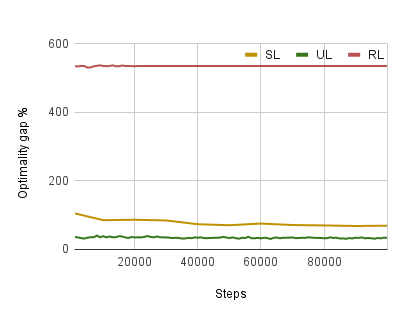
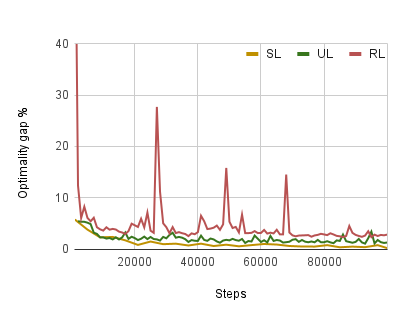
There has been a growing number of machine learning methods for approximately solving the travelling salesman problem. However, these methods often require solved instances for training or use complex reinforcement learning approaches that need a large amount of tuning. To avoid these problems, we introduce a novel unsupervised learning approach. We use a relaxation of an integer linear program for TSP to construct a loss function that does not require correct instance labels. With variable discretization, its minimum coincides with the optimal or near-optimal solution. Furthermore, this loss function is differentiable and thus can be used to train neural networks directly. We use our loss function with a Graph Neural Network and design controlled experiments on both Euclidean and asymmetric TSP. Our approach has the advantage over supervised learning of not requiring large labelled datasets. In addition, the performance of our approach surpasses reinforcement learning for asymmetric TSP and is comparable to reinforcement learning for Euclidean instances. Our approach is also more stable and easier to train than reinforcement learning.
翻译:大约解决流动销售商问题的机器学习方法越来越多,但是,这些方法往往需要解决培训或使用需要大量调整的复杂强化学习方法。为避免这些问题,我们采用了一种新型的、不受监督的学习方法。我们为TSP使用一个整数线性程序来构建一个不需要正确实例标签的损失函数。随着差异的分散化,其最小值与最佳或近乎最佳的解决方案相吻合。此外,这一损失功能是可以区分的,因此可以直接用来培训神经网络。我们用一个图形神经网络来使用我们的损失功能,并在Euclidean和不对称的TSP上设计受控制的实验。我们的方法优势在于监督地学习不要求大标记数据集。此外,我们的方法的绩效超过了不对称 TSP的强化学习,与强化 Euclidean 实例的学习相似。我们的方法也比强化学习更加稳定和容易培训。