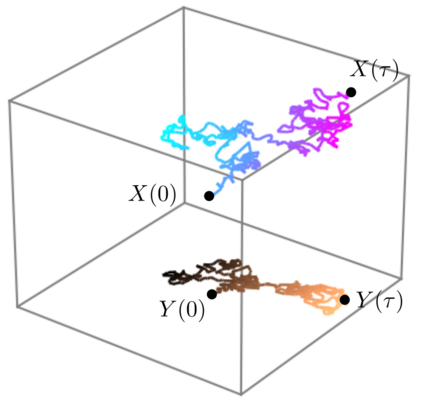
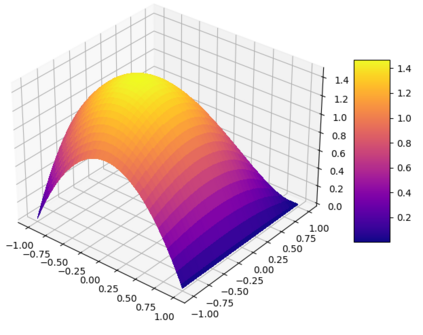
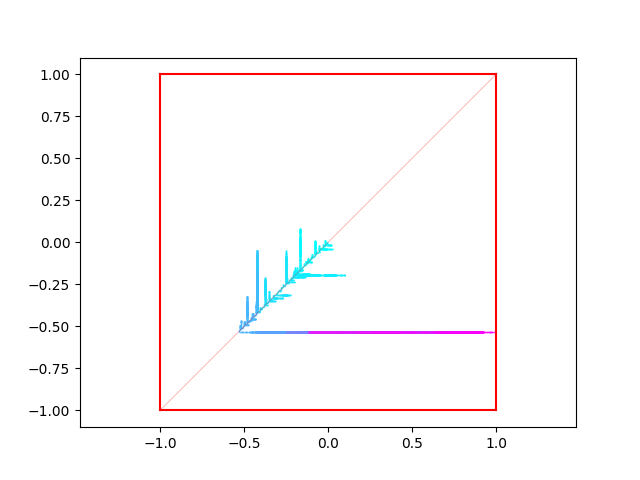
We introduce the notion of classical fractional query algorithms, which generalize decision trees in the average-case setting, and can potentially perform better than them. We show that the limiting run-time complexity of a natural class of these algorithms obeys the non-linear partial differential equation $\min_{k}\partial^{2}u/\partial x_{k}^{2}=-2$, and that the individual bit revealment satisfies the Schramm-Steif bound for Fourier weight, connecting noise sensitivity with PDEs. We discuss relations with other decision tree results.
翻译：我们引入了古典的分数查询算法概念,这种算法在平均情况中将决策树普遍化,并有可能比这些算法发挥更好的作用。 我们表明,这些算法的自然类别有限的运行时间复杂性符合非线性部分差分方程式 $\ min ⁇ k ⁇ k ⁇ q ⁇ 2}u/\ party x ⁇ k ⁇ 2 ⁇ 2 ⁇ 2 ⁇ 2$-2$, 个人比分法满足了Schramm-steif对Fourier重量的要求,将噪音敏感度与PDEs联系起来。我们讨论的是与其他决策树结果的关系。
相关内容
微信扫码咨询专知VIP会员