OlymMATH: 奥林匹克级双语数学基准，R1 正确率仅为 21.2%

摘要

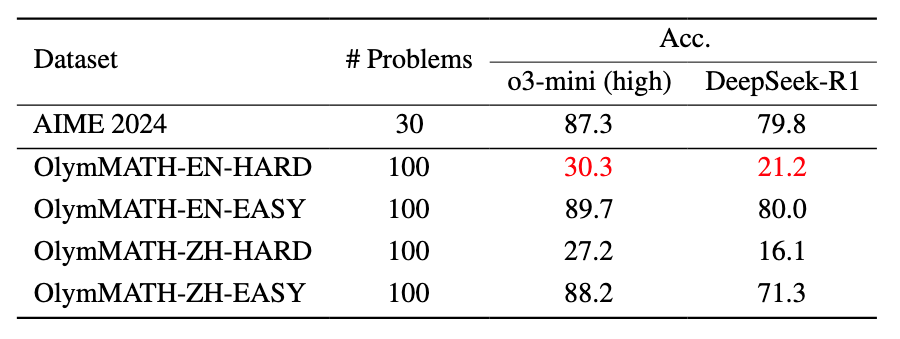
当前数学基准难以有效区分先进大模型的真实推理能力。为此，我们提出OlymMATH——一个奥林匹克级数学基准，包含200道高质量问题，并提供中英双语版本。OlymMATH分为easy和hard两个难度级别，其中easy子集的难度与AIME（美国数学邀请赛）对齐，hard子集则聚焦于更复杂的推理能力。实验表明，即使是最先进的模型，如DeepSeek-R1和o3-mini，在英文版hard数据集上的正确率仅为21.2%和30.3%。

论文题目：Challenging the Boundaries of Reasoning: An Olympiad-Level Math Benchmark for Large Language Models 论文链接：https://arxiv.org/abs/2503.21380 代码仓库：https://github.com/RUCAIBox/OlymMATH 数据集：https://huggingface.co/datasets/RUC-AIBOX/OlymMATH

简介

近年来，大型语言模型（LLMs）在数学推理任务上取得了显著进展。例如，OpenAI 的 o3-mini、DeepSeek-R1 和 QwQ 等模型已展现出卓越的数学解题能力。然而，现有数学基准（如 MATH 和 AIME）已不足以细粒度地区分最先进模型的能力差异，且其测试结果正逐步趋于饱和。此外，大多数现有基准仅提供英文数据，缺乏对 LLMs 在多语言环境下的系统性评估。为此，我们提出 OlymMATH，一个全新的奥林匹克级数学基准，旨在全面评估大模型的推理能力。与从网络爬取数据构建的基准不同，OlymMATH 依托高质量印刷资料（如数学竞赛杂志、教材及官方竞赛题库）精心筛选问题，以确保题目的原创性、挑战性和多样性。该基准涵盖 200 道高质量数学题，分为简单和困难两个子集，并提供完全平行的中英双语版本，以支持严格的多语言评估。这使得 OlymMATH 能够揭示语言对 LLM 数学推理能力的影响，并为未来研究提供更具深度的测评框架。

构建方法

OlymMATH 的构建过程涉及以下关键环节： * 数据筛选：从印刷资料中精选 200 道奥林匹克级数学题，避免使用在线资源，以最大程度降低数据污染风险。 * 题目分类与难度分级：OlymMATH 覆盖代数、几何、数论和组合数学四大数学领域，并按难度分为简单（EASY）和困难（HARD）两级。其中，EASY 级别与 AIME 竞赛题目难度相当，而 HARD 级别则测试模型的深度推理能力。 * 格式标准化与答案验证：OlymMATH 采用与 MATH 数据集相同的格式，以便于评估。此外，我们严格限定答案格式，仅包含实数和区间，排除难以验证的集合操作或符号表达式，确保评测的客观性。对于多个可能解的题目，我们对问题进行了改写，以要求模型解出所有可能的正确答案，从而考察其全面推理能力。 * 双语扩展：OlymMATH 包含完全对等的中英文问题集。英语版本采用 LLM + 人工审核的高质量翻译流程：首先由 Claude Sonnet 3.7 生成初步英文翻译，随后使用 GPT-4o 进行多轮优化，最后由专家审核，确保英语版本的可靠性。

实验结果

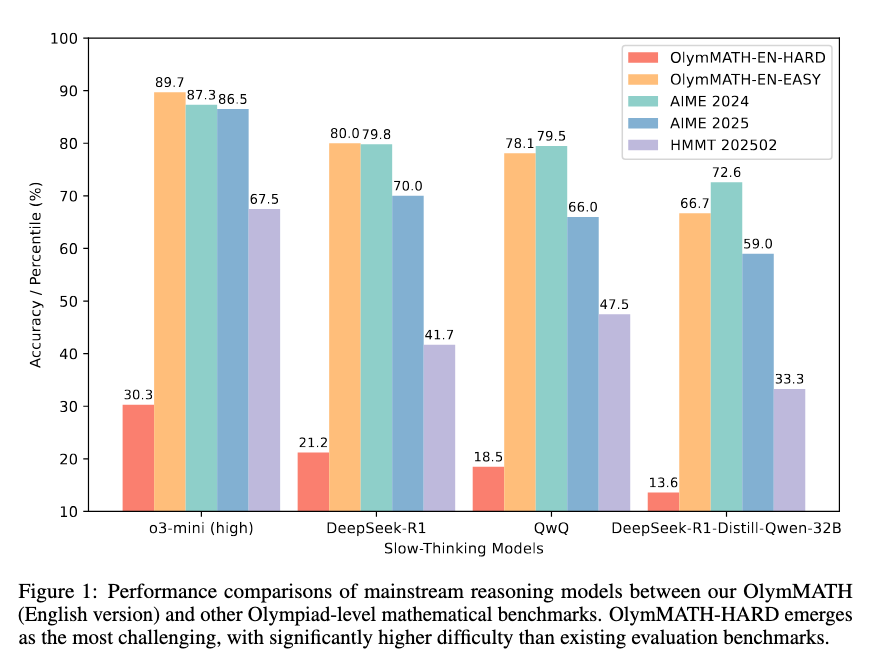
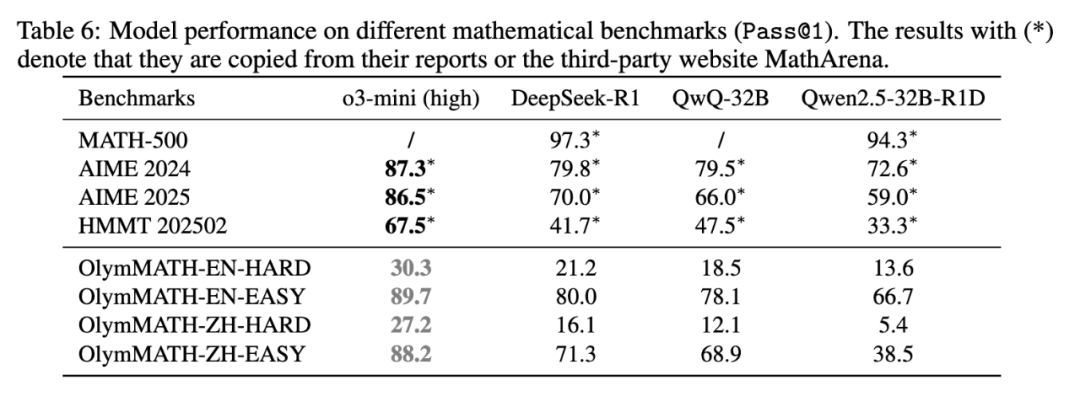
🚀 我们的实验表明： * OlymMATH 比现有数学基准更具挑战性。例如，即使是顶尖模型 OpenAI o3-mini (high)，在 OlymMATH-EN-HARD 上的准确率也仅为 30.3%，而其他模型在 MATH-500 和 AIME 2024 等现有基准上的准确率通常在 70%-90% 之间。 * OlymMATH 能更好区分模型能力。在 MATH-500 上，DeepSeek-R1 和 Qwen2.5-32B-R1D 的准确率非常接近（97.3% vs 94.3%），但在 OlymMATH-EN-HARD 上，两者的准确率分别下降至 21.2% 和 13.6%，表明 OlymMATH 在区分不同模型的推理能力方面更具优势。

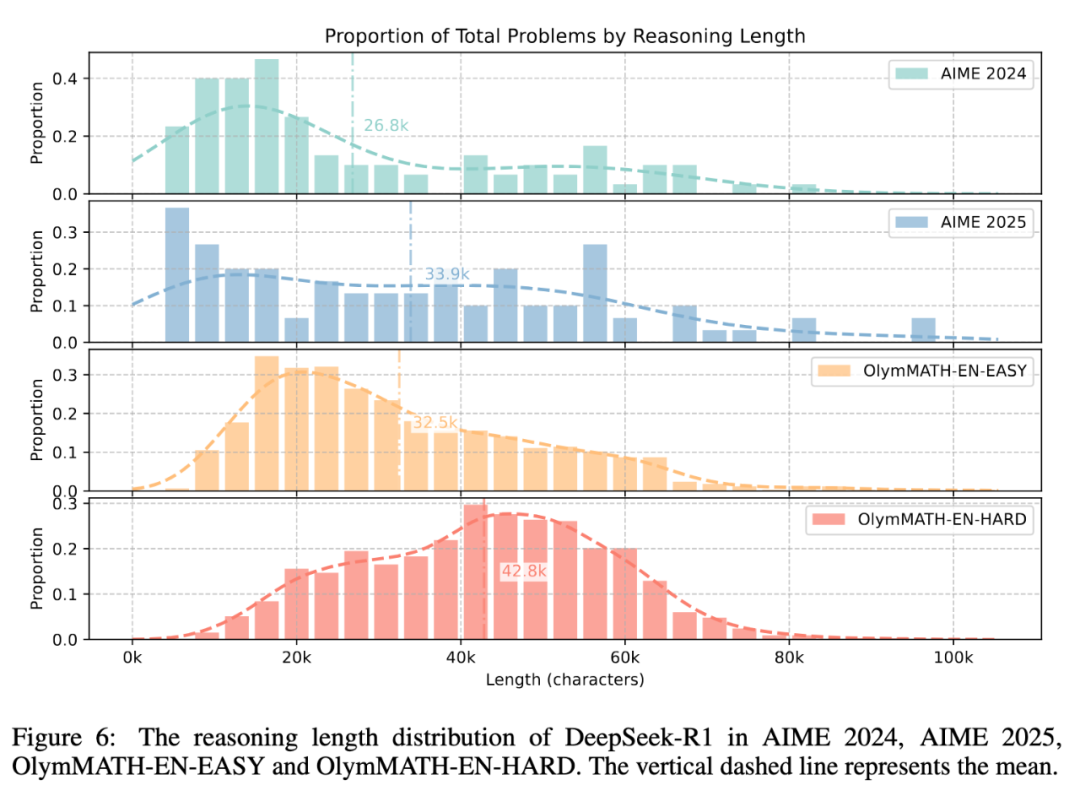
语言对推理能力有显著影响。所有模型在英文基准上的表现均优于中文基准，这一现象表明语言对 LLM 数学推理能力可能存在显著影响，进一步强调了多语言评估的重要性。 * 同时我们进行了对 DeepSeek-R1 的思维链长度的分析。实验结果表明，从思维链长度的分布来看，OlymMATH-EASY 与 AIME 具有类似的难度，而 OlymMATH-HARD 则包含更多的挑战性题目。