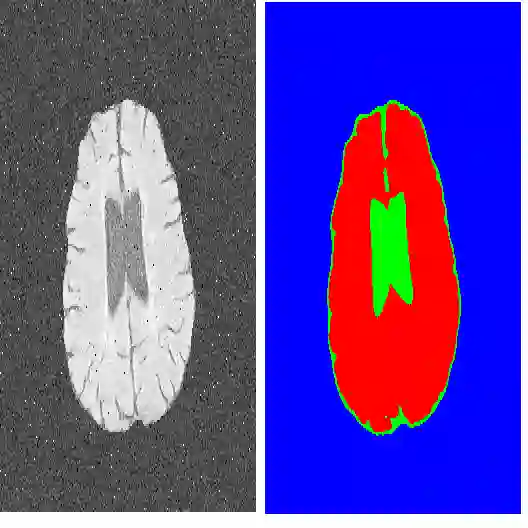
Minimizing a sum of simple submodular functions of limited support is a special case of general submodular function minimization that has seen numerous applications in machine learning. We develop fast techniques for instances where components in the sum are cardinality-based, meaning they depend only on the size of the input set. This variant is one of the most widely applied in practice, encompassing, e.g., common energy functions arising in image segmentation and recent generalized hypergraph cut functions. We develop the first approximation algorithms for this problem, where the approximations can be quickly computed via reduction to a sparse graph cut problem, with graph sparsity controlled by the desired approximation factor. Our method relies on a new connection between sparse graph reduction techniques and piecewise linear approximations to concave functions. Our sparse reduction technique leads to significant improvements in theoretical runtimes, as well as substantial practical gains in problems ranging from benchmark image segmentation tasks to hypergraph clustering problems.
翻译:最大限度地减少有限支持的简单亚模块功能,是一般子模块功能最小化的一个特例,在机器学习中有许多应用。我们开发了快速技术,处理以基本内容为基础的组件,这意味着这些组件仅取决于输入集的大小。这一变式是实践中应用最广泛的一种,包括图像分割和最近普遍高压切除功能中产生的共同能源功能。我们为此问题开发了第一个近似算法,通过将近似值减为稀薄的图形切除问题,快速计算近似值,而图形孔径则由理想的近似系数控制。我们的方法依赖于稀有图形减少技术和小片线性线性近似线性功能之间的新连接。我们稀有的减少技术导致理论运行时间的重大改进,以及在从基准图像分割任务到超光速组合问题等问题上取得大量实际收益。