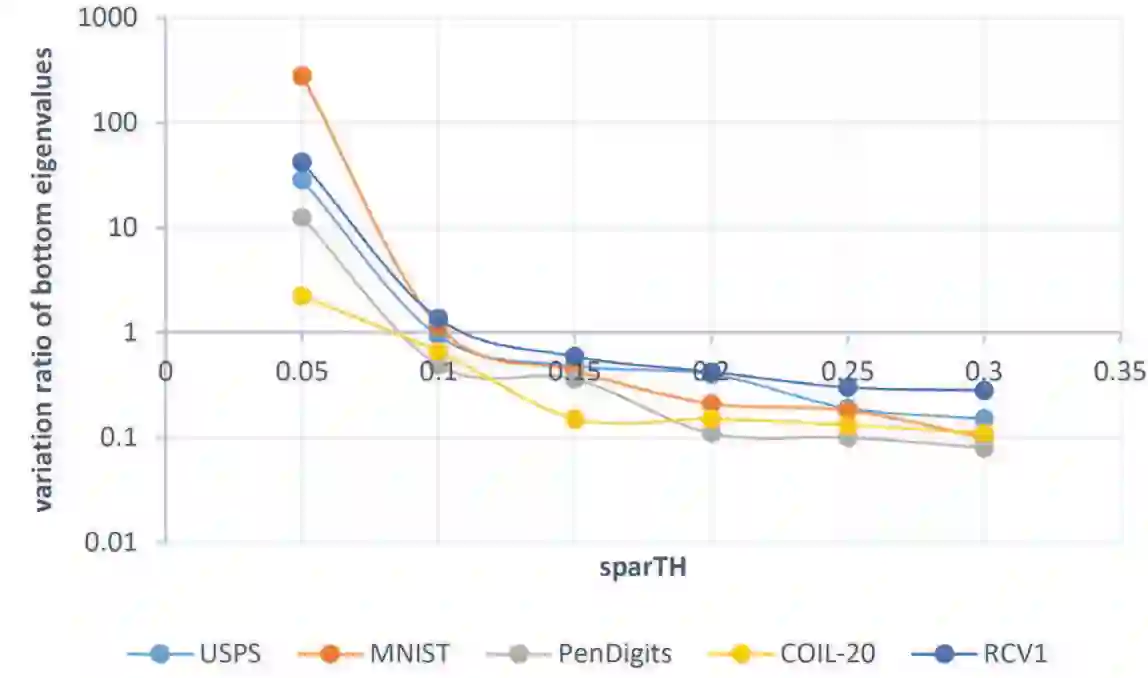
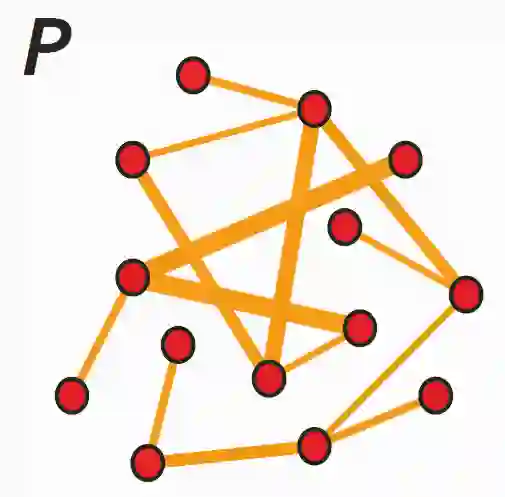
The eigendeomposition of nearest-neighbor (NN) graph Laplacian matrices is the main computational bottleneck in spectral clustering. In this work, we introduce a highly-scalable, spectrum-preserving graph sparsification algorithm that enables to build ultra-sparse NN (u-NN) graphs with guaranteed preservation of the original graph spectrums, such as the first few eigenvectors of the original graph Laplacian. Our approach can immediately lead to scalable spectral clustering of large data networks without sacrificing solution quality. The proposed method starts from constructing low-stretch spanning trees (LSSTs) from the original graphs, which is followed by iteratively recovering small portions of "spectrally critical" off-tree edges to the LSSTs by leveraging a spectral off-tree embedding scheme. To determine the suitable amount of off-tree edges to be recovered to the LSSTs, an eigenvalue stability checking scheme is proposed, which enables to robustly preserve the first few Laplacian eigenvectors within the sparsified graph. Additionally, an incremental graph densification scheme is proposed for identifying extra edges that have been missing in the original NN graphs but can still play important roles in spectral clustering tasks. Our experimental results for a variety of well-known data sets show that the proposed method can dramatically reduce the complexity of NN graphs, leading to significant speedups in spectral clustering.
翻译:近邻图形( NN) 图形 Laplacian 矩阵的 eigendemposition 是光谱群集中主要的计算瓶颈。 在这项工作中, 我们引入了一个高度可缩放的、 保存频谱的图形宽度算法, 通过利用光谱离树嵌入方案, 可以在原始图形频谱中建立超开放的 NN( u- NN) 图形, 比如原始图 Laplacian 的最初几小位离岸边缘。 我们的方法可以立即导致大型数据网络的可缩放频谱集, 而不会牺牲解决方案的质量。 提议的方法是从原始图表中构建低伸缩的覆盖树( LSST) 。 之后, 通过利用光谱离树层嵌入方案, 能够反复恢复“ 光谱关键” 离岸边缘的极小部分。 为了确定我们原始的图像平面图中的重要的渐变数, 也可以在原始的平面图中, 将提议的渐渐变的渐变的图像显示结果。