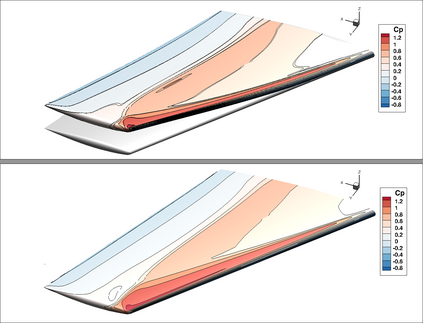
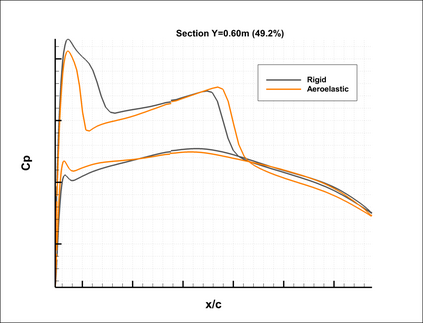
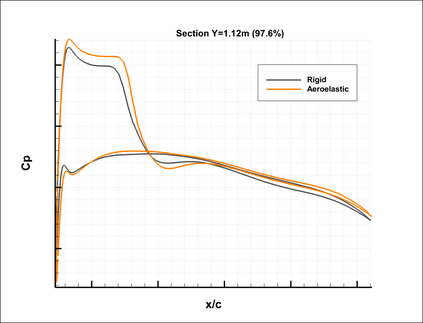
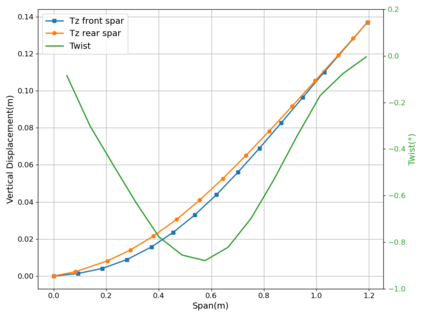
Robust and efficient solvers for coupled-adjoint linear systems are crucial to successful aerostructural optimization. Monolithic and partitioned strategies can be applied. The monolithic approach is expected to offer better robustness and efficiency for strong fluid-structure interactions. However, it requires a high implementation cost and convergence may depend on appropriate scaling and initialization strategies. On the other hand, the modularity of the partitioned method enables a straightforward implementation while its convergence may require relaxation. In addition, a partitioned solver leads to a higher number of iterations to get the same level of convergence as the monolithic one. The objective of this paper is to accelerate the fluid-structure coupled-adjoint partitioned solver by considering techniques borrowed from approximate invariant subspace recycling strategies adapted to sequences of linear systems with varying right-hand sides. Indeed, in a partitioned framework, the structural source term attached to the fluid block of equations affects the right-hand side with the nice property of quickly converging to a constant value. We also consider deflation of approximate eigenvectors in conjunction with advanced inner-outer Krylov solvers for the fluid block equations. We demonstrate the benefit of these techniques by computing the coupled derivatives of an aeroelastic configuration of the ONERA-M6 fixed wing in transonic flow. For this exercise the fluid grid was coupled to a structural model specifically designed to exhibit a high flexibility. All computations are performed using RANS flow modeling and a fully linearized one-equation Spalart-Allmaras turbulence model. Numerical simulations show up to 39% reduction in matrix-vector products for GCRO-DR and up to 19% for the nested FGCRO-DR solver.
翻译:暂无翻译