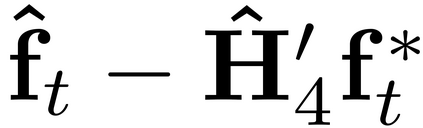
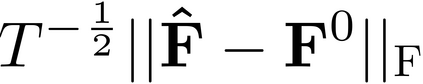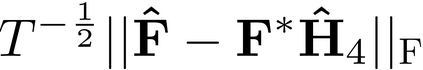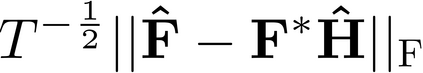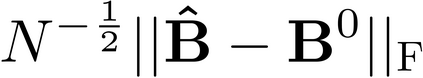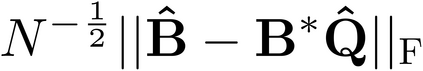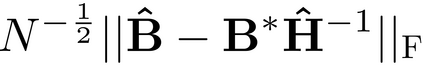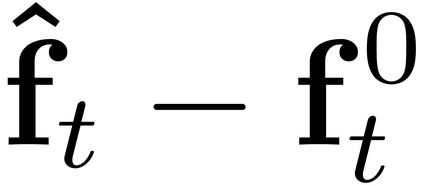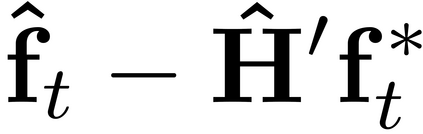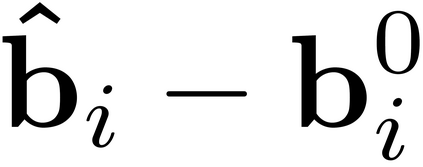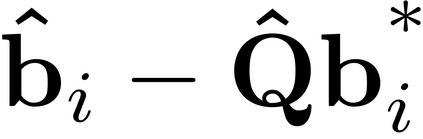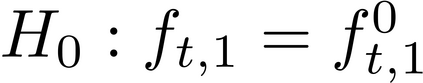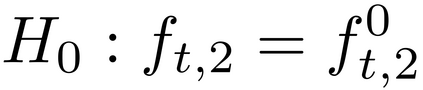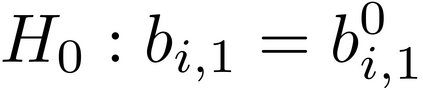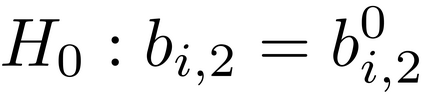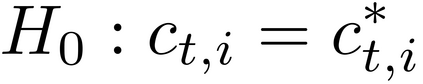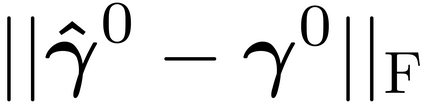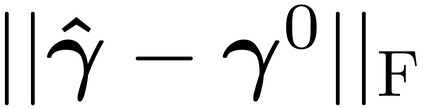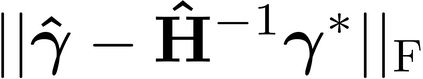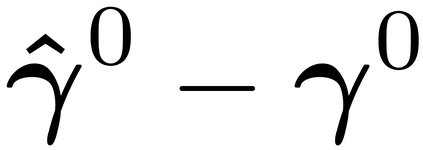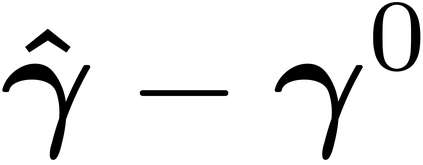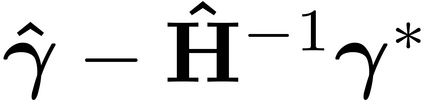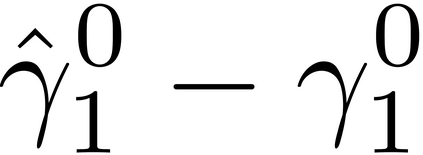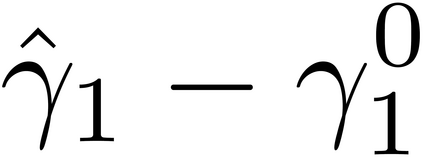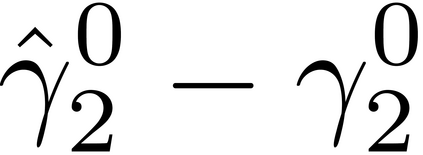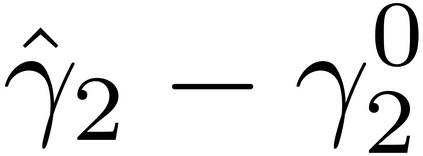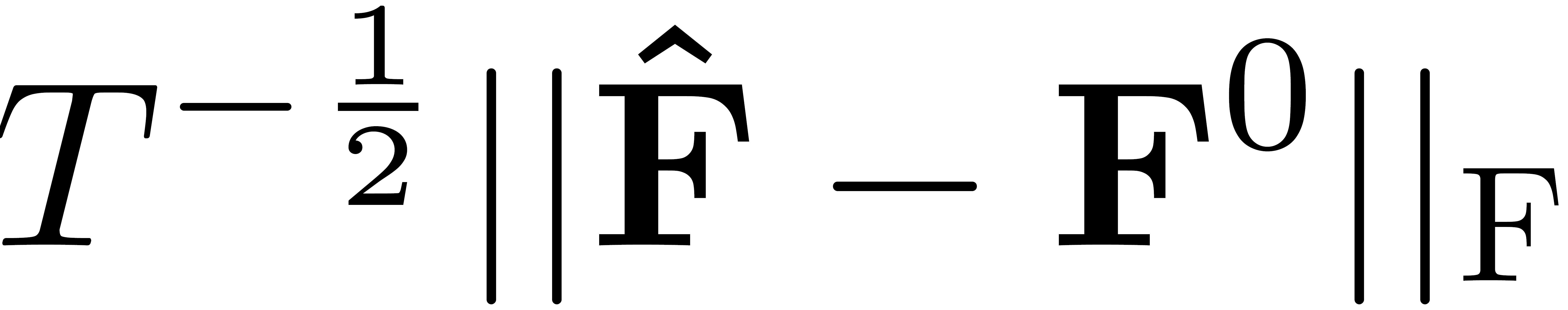It is well-known that the approximate factor models have the rotation indeterminacy. It has been considered that the principal component (PC) estimators estimate some rotations of the true factors and factor loadings, but the rotation matrix commonly used in the literature depends on the PC estimator itself. This raises a question: what does the PC estimator consistently estimate? This paper aims to explore the answer. We first show that, assuming a quite general weak factor model with the $r$ signal eigenvalues diverging possibly at different rates, there always exists a unique rotation matrix composed only of the true factors and loadings, such that it rotates the true model to the identifiable model satisfying the standard $r^2$ restrictions. We call the rotated factors and loadings the pseudo-true parameters. We next establish the consistency and asymptotic normality of the PC estimator for this pseudo-true parameter. The results give an answer for the question: the PC estimator consistently estimates the pseudo-true parameter. We also investigate similar problems in the factor augmented regression. Finite sample experiments confirm the excellent approximation of the theoretical results.
翻译:暂无翻译