Are Normalizing Flows the Key to Unlocking the Exponential Mechanism? A Path through the Accuracy-Privacy Ceiling Constraining Differentially Private ML

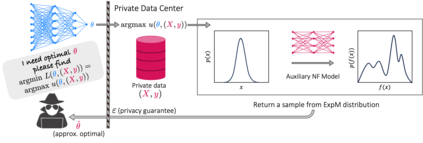
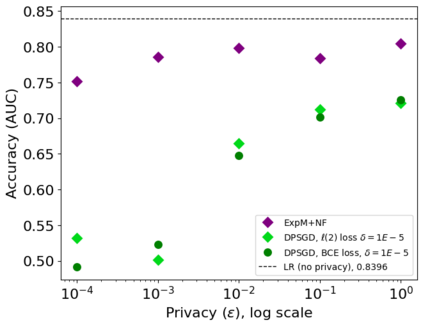
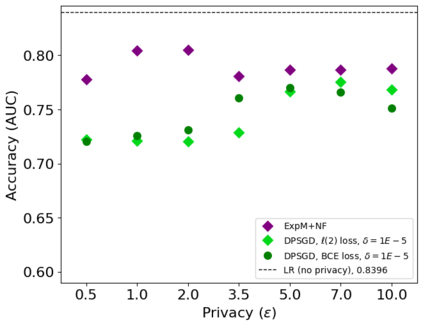
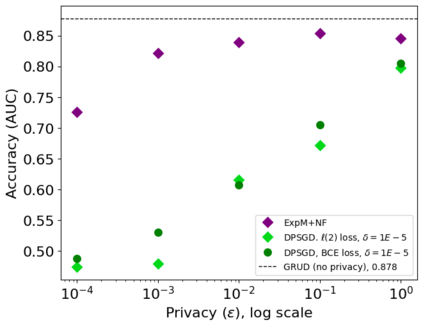
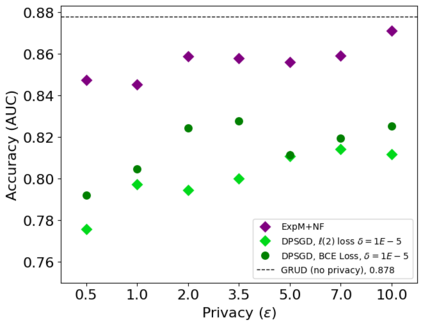
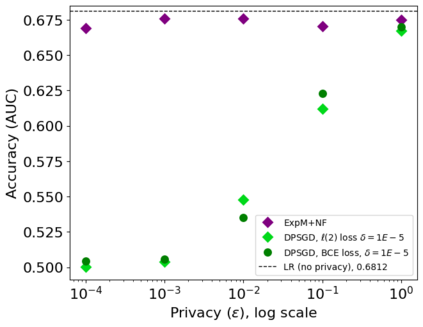
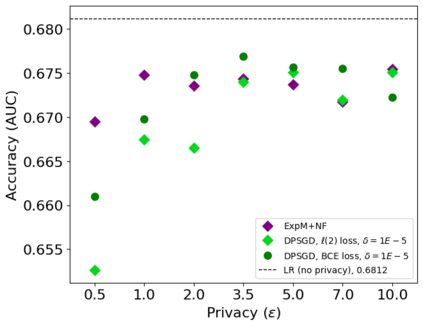
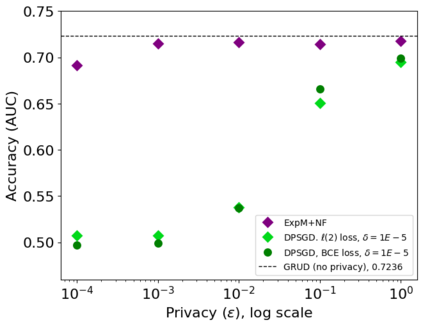
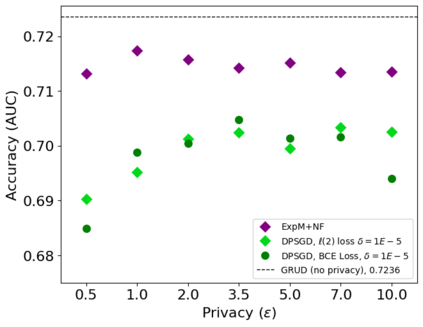
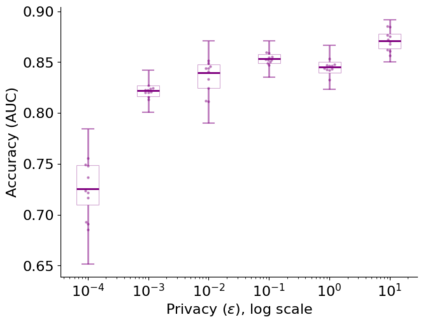
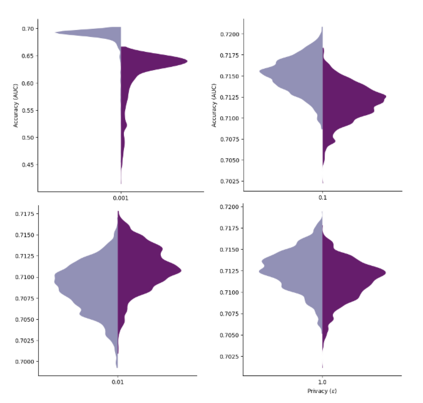
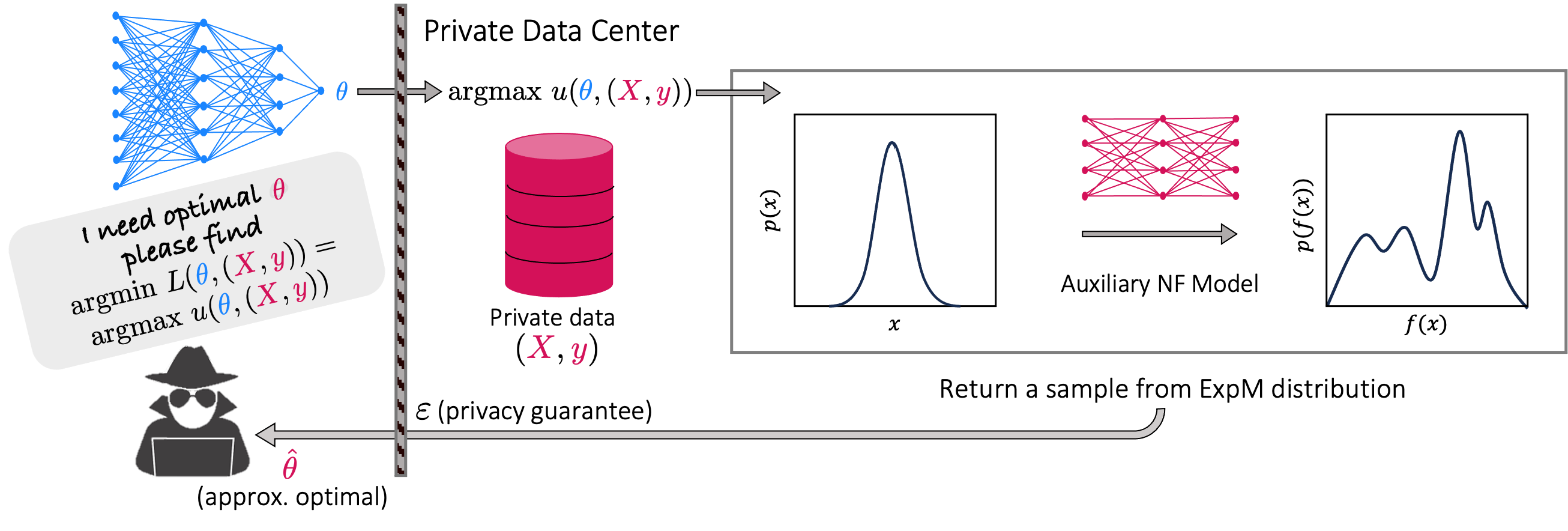
The state of the art and de facto standard for differentially private machine learning (ML) is differentially private stochastic gradient descent (DPSGD). Yet, the method is inherently wasteful. By adding noise to every gradient, it diminishes the overall privacy with every gradient step. Despite 15 years of fruitful research advancing the composition theorems, sub-sampling methods, and implementation techniques, adequate accuracy and privacy is often unattainable with current private ML methods. Meanwhile, the Exponential Mechanism (ExpM), designed for private optimization, has been historically sidelined from privately training modern ML algorithms primarily because ExpM requires sampling from a historically intractable density. Despite the recent discovery of Normalizing Flow models (NFs), expressive deep networks for approximating intractable distributions, ExpM remains in the background. Our position is that leveraging NFs to circumvent historic obstructions of ExpM is a potentially transformational solution for differentially private ML worth attention. We introduce a new training method, ExpM+NF, as a potential alternative to DPSGD, and we provide experiment with logistic regression and a modern deep learning model to test whether training via ExpM+NF is viable with "good" privacy parameters. Under the assumption that the NF output distribution is the ExpM distribution, we are able to achieve $\varepsilon$ a low as $1\mathrm{e}{-3}$ -- three orders of magnitude stronger privacy with similar accuracy. This work outlines a new avenue for advancing differentially private ML, namely discovering NF approximation guarantees. Code to be provided after review.