A Fast Algorithm for Implementation of Some Minimum L2 Distance Estimators and Their Application to Image Segmentation

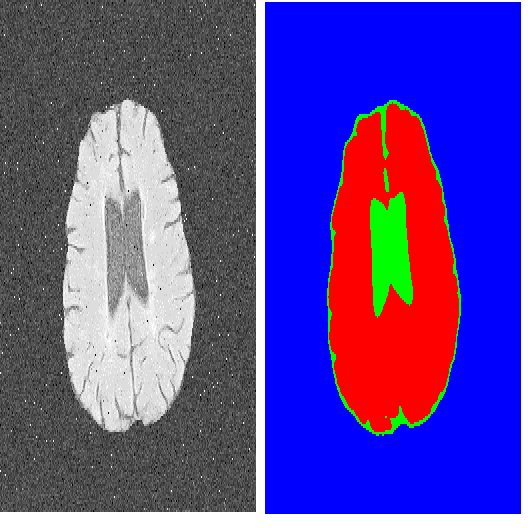
Minimum distance estimation methodology based on empirical distribution function has been popular due to its desirable properties including robustness. Even though the statistical literature is awash with the research on the minimum distance estimation, the most of it is confined to the theoretical findings: only few statisticians conducted research on the application of the method to real world problems. Through this paper, we extend the domain of application of this methodology to various applied fields by providing a solution to a rather challenging and complicated computational problem. The problem this paper tackles is an image segmentation which has been used in various fields. We propose a novel method based on the classical minimum distance estimation theory to solve the image segmentation problem. The performance of the proposed method is then further elevated by integrating it with the "segmenting-together" strategy.