On Grobner-Shirshov bases for Markov semirings

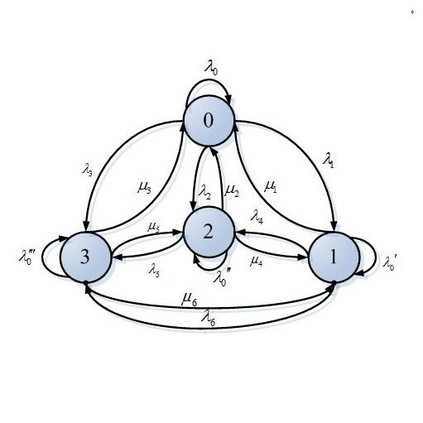
In order to investigate the relationship between Shannon information measure of random variables, scholars such as Yeung utilized information diagrams to explore the structured representation of information measures, establishing correspondences with sets. However, this method has limitations when studying information measures of five or more random variables. In this paper, we consider employing algebraic methods to study the relationship of information measures of random variables. By introducing a semiring generated by random variables, we establish correspondences between sets and elements of the semiring. Utilizing the Grobner-Shirshov basis, we present the structure of the semiring and its standard form. Furthermore, we delve into the structure of the semiring generated under Markov chain conditions (referred to as Markov semiring), obtaining its standard form.