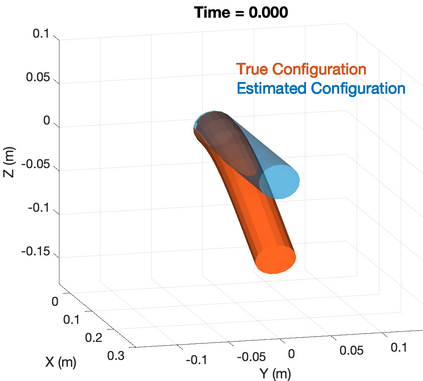
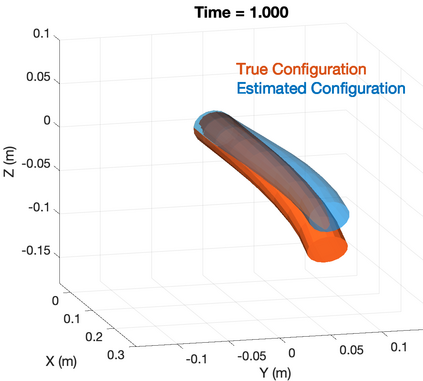
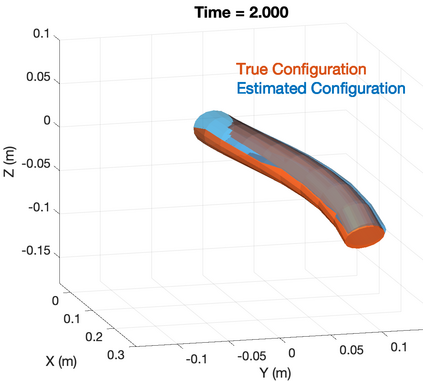
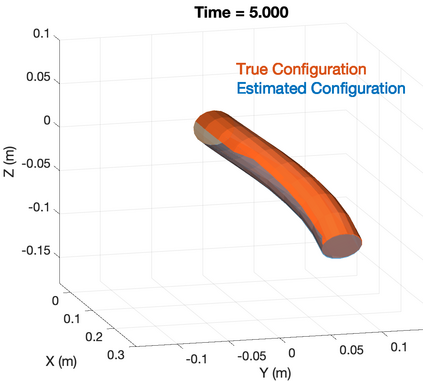
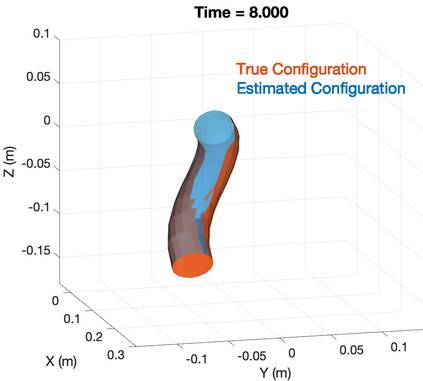
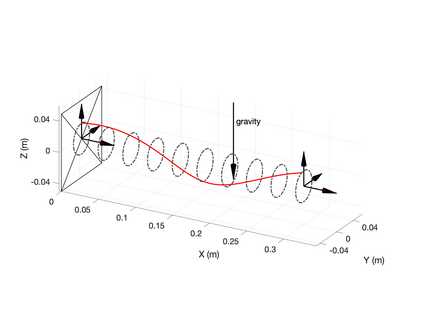
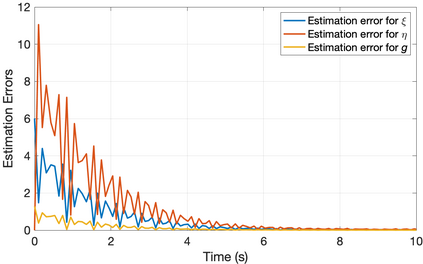
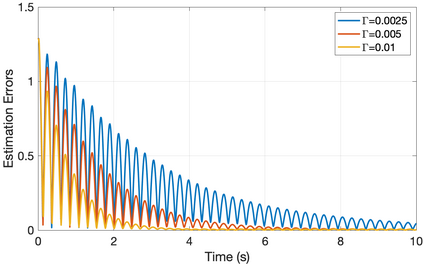
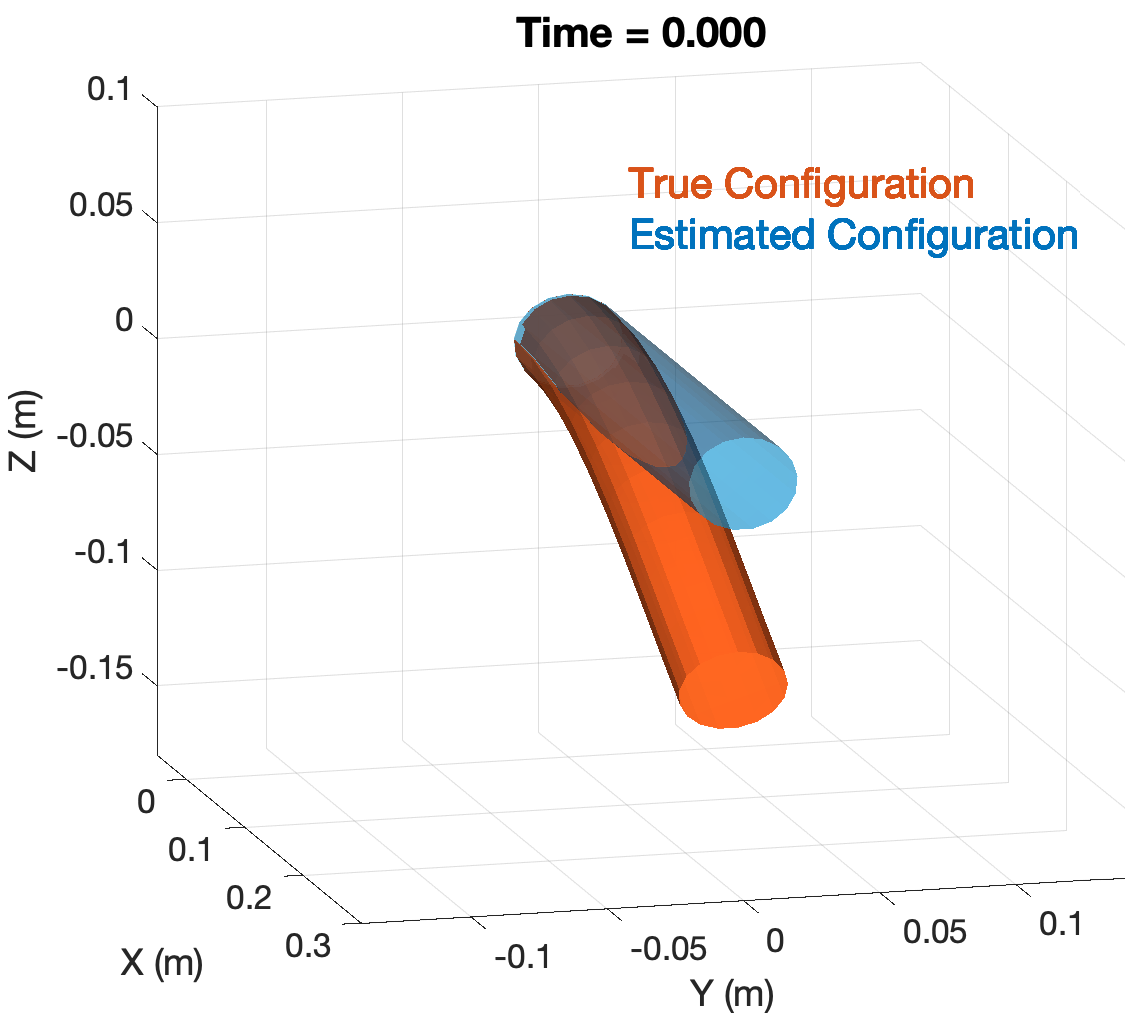
Soft robotics is a rapidly growing research area in robotics. Sensing of robotic systems is important for designing feedback controllers which usually provide robustness to modeling uncertainties. Sensing of soft robots, however, is considered a challenging task because theoretically, soft robots have infinite degrees of freedom while existing sensors only provide a limited number of measurements. One solution to this challenge is to design an observer/filter to estimate the unknown states from the sensor measurements. In this work, we design a boundary observer for soft robots based on the well-known Cosserat rod theory which models soft robots by nonlinear partial differential equations (PDEs). This boundary observer is able to estimate all the continuous robot states (poses, strains, and velocities) using the PDE model, inputs, and only tip velocity measurements (which explains the name "boundary" observer). The key idea is to inject sequential tip velocity measurements into the observer in a way that dissipates the energy of state estimation errors through the boundary. This boundary observer only requires sensing the tip velocity, can be implemented by simply changing a boundary condition in any numerical solvers of Cosserat rod models, and is proven to be locally input-to-state stable. Simulation studies are included and suggest that the domain of attraction is large and the observer is robust to measurement noise.
翻译:软软机器人是机器人中一个快速增长的研究领域。 机器人系统的遥感对于设计反馈控制器非常重要, 后者通常能为建模的不确定性提供稳健性。 但是, 软机器人的遥感被认为是一项具有挑战性的任务, 因为理论上软机器人拥有无限的自由度, 而现有的传感器只能提供数量有限的测量。 这一挑战的一个解决办法是设计一个观察者/ 过滤者来估计传感器测量的未知状态。 在这项工作中, 我们设计一个软机器人的边界观察者, 以众所周知的 Cosserat 鼠标理论为基础, 以非线性部分偏差方程式( PDEs) 模拟软机器人。 这个边界观察者能够使用PDE 模型、 投入和仅限量度测量小数速度的测量方法来估计所有连续机器人状态( 位置、 强度和速度) 。 关键的想法是设计一个观察者来向观察者输入测算测算测算测算测算测算测算测算测算测算器的能量, 这个测算器只需通过非线性部分偏差方方方方方方方方方程式来测测算,, 只需改变一个连续的边界状态状态状态状态状态状态状态状态状态状态状态状态状态状态状态状态状态状态状态状况,, 。</s>