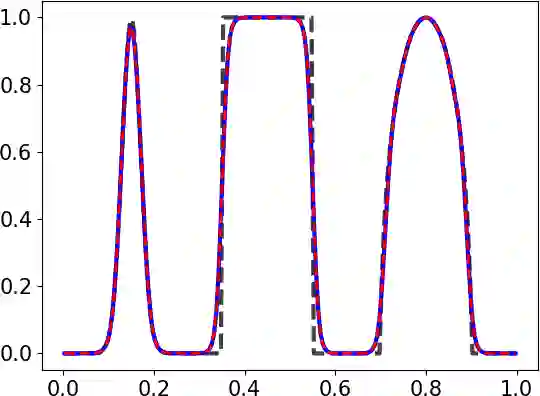
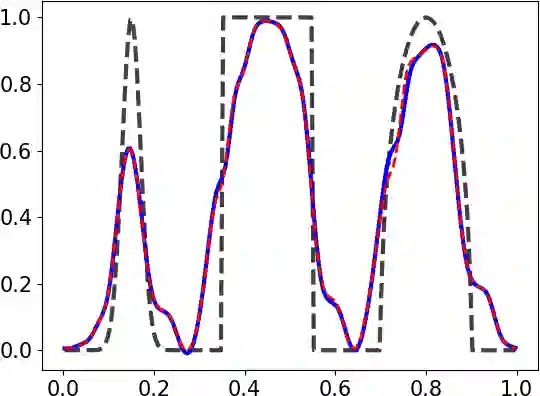
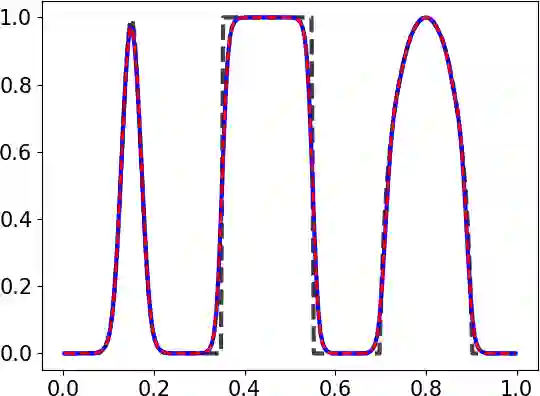
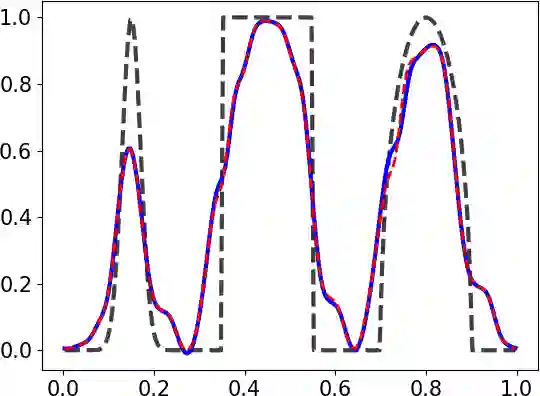
We introduce a general framework for enforcing local or global maximum principles in high-order space-time discretizations of a scalar hyperbolic conservation law. We begin with sufficient conditions for a space discretization to be bound preserving (BP) and satisfy a semi-discrete maximum principle. Next, we propose a global monolithic convex (GMC) flux limiter which has the structure of a flux-corrected transport (FCT) algorithm but is applicable to spatial semi-discretizations and ensures the BP property of the fully discrete scheme for strong stability preserving (SSP) Runge-Kutta time discretizations. To circumvent the order barrier for SSP time integrators, we constrain the intermediate stages and/or the final stage of a general high-order RK method using GMC-type limiters. In this work, our theoretical and numerical studies are restricted to explicit schemes which are provably BP for sufficiently small time steps. The new GMC limiting framework offers the possibility of relaxing the bounds of inequality constraints to achieve higher accuracy at the cost of more stringent time step restrictions. The ability of the presented limiters to preserve global bounds and recognize well-resolved smooth solutions is verified numerically for three representative RK methods combined with weighted essentially nonoscillatory (WENO) finite volume space discretizations of linear and nonlinear test problems in 1D.
翻译:我们引入了一个总体框架,用于在高阶时空离散的超双曲线保护法中执行地方或全球最大原则。我们首先为空间离散以约束保存(BP)和满足半分解最大原则提出充分的条件,然后提出一个全球单流二次曲线通量限制(GMC),其结构是通量校正运输算法(FCT)算法,但适用于空间半分解,并确保完全离散的维护强稳(SSP)Runge-Kutta时间离散(Runge-Kutta时间离散)计划BP的特性。为了绕过SSP时间融合器的秩序障碍,我们用GMC型限制器限制中间阶段和/或一般高端RK方法的最后阶段。在这项工作中,我们的理论和数字研究限于明确的计划,这种计划在足够小的时间步骤中具有可调和可调的BP。新的GMC框架提供了放宽不平等限制的界限的可能性,以便在更严格的时间跨段限制下实现更精确的准确性,在更严格的时间跨步限制中,基本上保持了高水平检验方法。