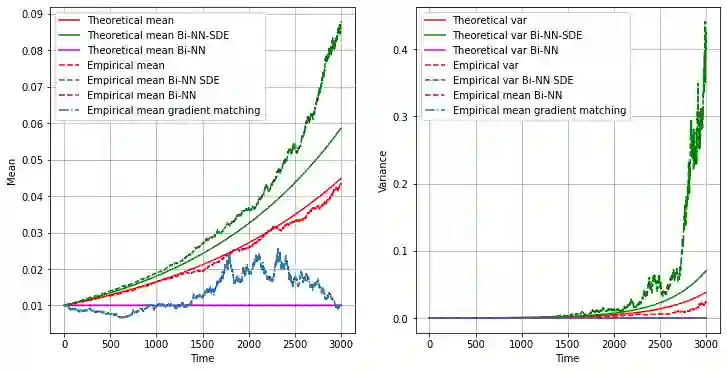
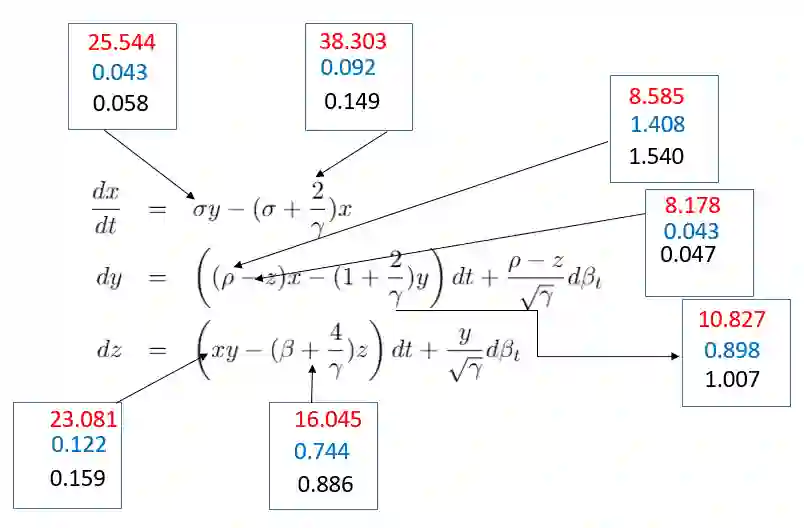
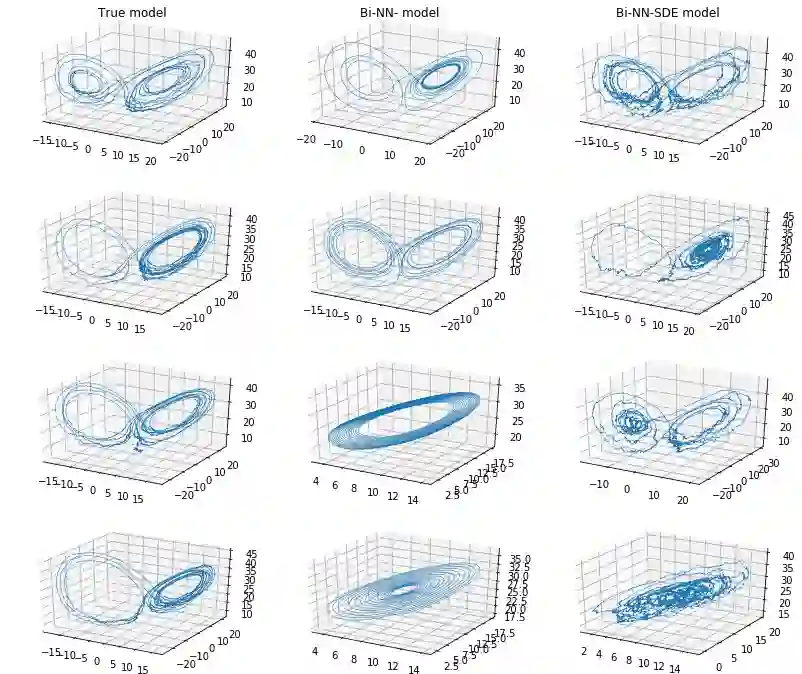
Stochastic differential equations (SDEs) are one of the most important representations of dynamical systems. They are notable for the ability to include a deterministic component of the system and a stochastic one to represent random unknown factors. However, this makes learning SDEs much more challenging than ordinary differential equations (ODEs). In this paper, we propose a data driven approach where parameters of the SDE are represented by a neural network with a built-in SDE integration scheme. The loss function is based on a maximum likelihood criterion, under order one Markov Gaussian assumptions. The algorithm is applied to the geometric brownian motion and a stochastic version of the Lorenz-63 model. The latter is particularly hard to handle due to the presence of a stochastic component that depends on the state. The algorithm performance is attested using different simulations results. Besides, comparisons are performed with the reference gradient matching method used for non linear drift estimation, and a neural networks-based method, that does not consider the stochastic term.
翻译:电磁微分方程式(SDEs)是动态系统最重要的体现形式之一,其显著之处在于能够包括系统中的确定性成分和代表随机未知因素的随机随机随机的随机随机随机偏差因素。然而,这使得学习SDEs比普通差异方程式(ODEs)更具挑战性。在本文中,我们提议了一种数据驱动方法,即SDE的参数由内建SDE集成计划神经网络代表。损失功能基于最大可能性标准,按Markov Gaussian 的顺序排列。算法应用于几何褐色运动和Lorenz-63模型的随机版。由于存在取决于状态的随机方程式,后者尤其难以处理。算法性表现通过不同的模拟结果得到证明。此外,还用非线性流估计所用的参考梯度匹配法和不考虑神经网络法术语的神经网络方法进行了比较。