Existence, uniqueness, and approximation of solutions of jump-diffusion SDEs with discontinuous drift

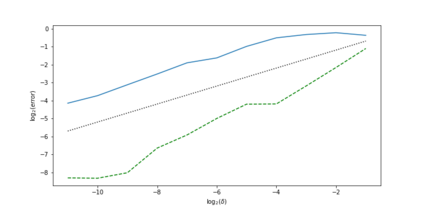
In this paper we study jump-diffusion stochastic differential equations (SDEs) with a discontinuous drift coefficient and a possibly degenerate diffusion coefficient. Such SDEs appear in applications such as optimal control problems in energy markets. We prove existence and uniqueness of strong solutions. In addition we study the strong convergence order of the Euler-Maruyama scheme and recover the optimal rate $1/2$.