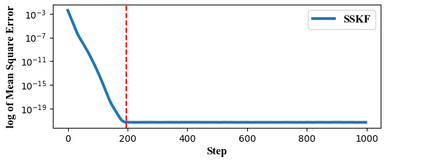
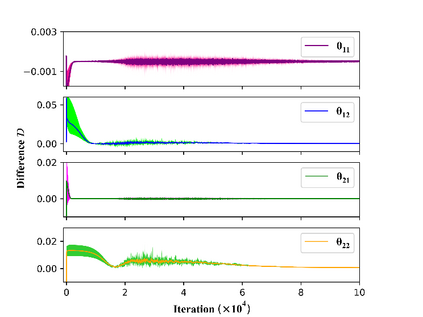
State estimation is critical to control systems, especially when the states cannot be directly measured. This paper presents an approximate optimal filter, which enables to use policy iteration technique to obtain the steady-state gain in linear Gaussian time-invariant systems. This design transforms the optimal filtering problem with minimum mean square error into an optimal control problem, called Approximate Optimal Filtering (AOF) problem. The equivalence holds given certain conditions about initial state distributions and policy formats, in which the system state is the estimation error, control input is the filter gain, and control objective function is the accumulated estimation error. We present a policy iteration algorithm to solve the AOF problem in steady-state. A classic vehicle state estimation problem finally evaluates the approximate filter. The results show that the policy converges to the steady-state Kalman gain, and its accuracy is within 2 %.
翻译:国家估算对于控制系统至关重要, 特别是当国家无法直接测量时。 本文展示了一种近似最佳的过滤器, 能够使用政策迭代技术获得线性高斯时间变量系统中的稳态增益。 设计将最小中值平方错误的最佳过滤问题转化为最佳控制问题, 称为“ 优化过滤( AOF) ” 问题 。 等值为初始状态分布和政策格式的某些条件, 其中系统表示的是估算错误, 控制输入是过滤增益, 控制目标功能是累积的估算错误。 我们提出了一个政策迭代算法, 以解决稳定状态中的 AOF 问题 。 典型的车辆状态估算问题最终评估了近似过滤器问题 。 结果表明, 政策与稳定状态 Kalman 收益相趋近, 其准确度在2% 。