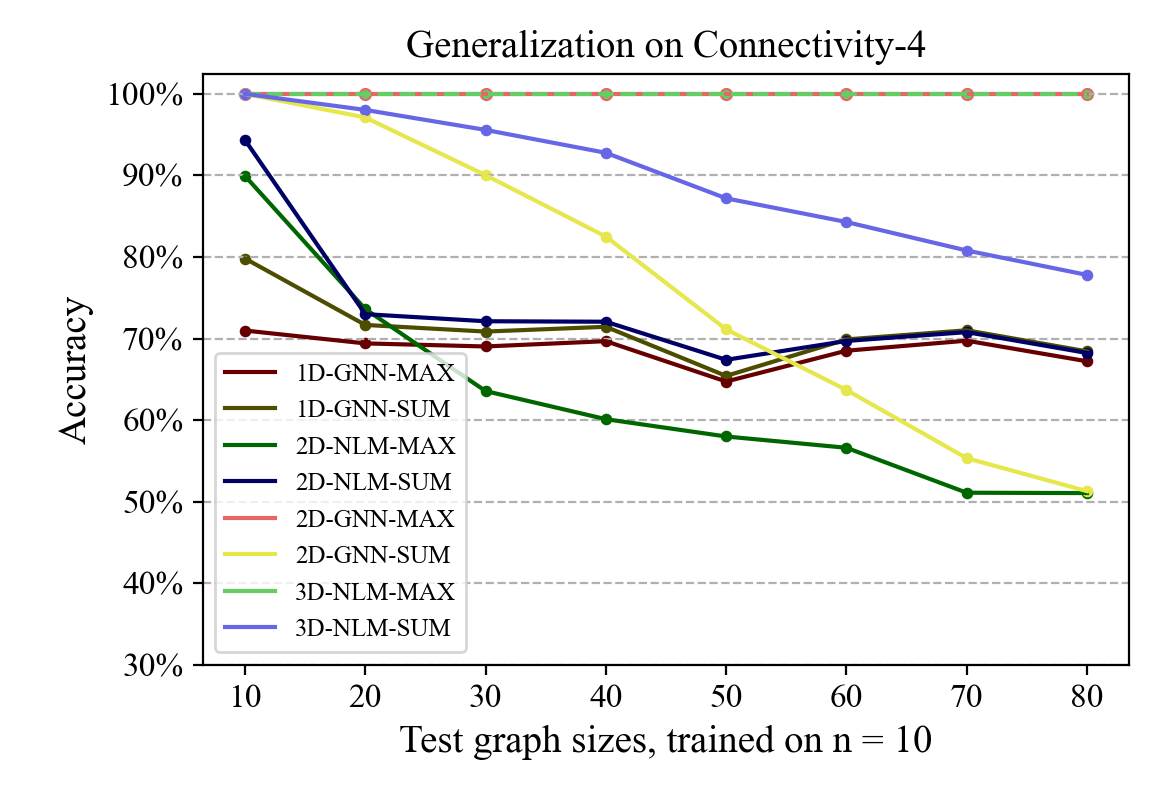
This extended abstract describes a framework for analyzing the expressiveness, learning, and (structural) generalization of hypergraph neural networks (HyperGNNs). Specifically, we focus on how HyperGNNs can learn from finite datasets and generalize structurally to graph reasoning problems of arbitrary input sizes. Our first contribution is a fine-grained analysis of the expressiveness of HyperGNNs, that is, the set of functions that they can realize. Our result is a hierarchy of problems they can solve, defined in terms of various hyperparameters such as depths and edge arities. Next, we analyze the learning properties of these neural networks, especially focusing on how they can be trained on a finite set of small graphs and generalize to larger graphs, which we term structural generalization. Our theoretical results are further supported by the empirical results.
翻译:这个扩展的抽象描述一个分析超光速神经网络(HyperGNNSs)的表达性、学习性和(结构性)一般化的框架。 具体地说, 我们侧重于超光速GNNs如何从有限的数据集中学习, 从结构上概括到任意输入大小的推理问题。 我们的第一个贡献是对超光速GNNs的表达性进行精细分析, 也就是他们能够实现的功能组。 我们的结果是他们能够解决的问题的层次分级, 以深度和边缘等各种超光度计来定义。 接下来, 我们分析这些神经网络的学习性质, 特别是如何对他们进行关于小图表的有限化培训, 并概括到更大的图形, 我们称之为结构上的概括。 我们的理论结果得到了经验结果的进一步支持。</s>