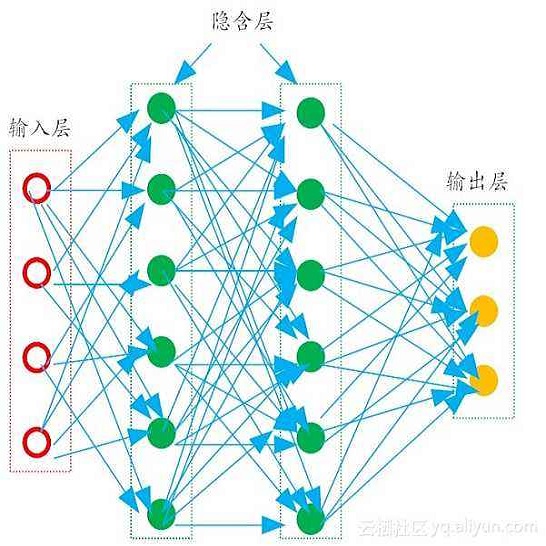
Model Order Reduction (MOR) methods enable the generation of real-time-capable digital twins, which can enable various novel value streams in industry. While traditional projection-based methods are robust and accurate for linear problems, incorporating Machine Learning to deal with nonlinearity becomes a new choice for reducing complex problems. Such methods usually consist of two steps. The first step is dimension reduction by projection-based method, and the second is the model reconstruction by Neural Network. In this work, we apply some modifications for both steps respectively and investigate how they are impacted by testing with three simulation models. In all cases Proper Orthogonal Decomposition (POD) is used for dimension reduction. For this step, the effects of generating the input snapshot database with constant input parameters is compared with time-dependent input parameters. For the model reconstruction step, two types of neural network architectures are compared: Multilayer Perceptron (MLP) and Runge-Kutta Neural Network (RKNN). The MLP learns the system state directly while RKNN learns the derivative of system state and predicts the new state as a Runge-Kutta integrator.
翻译:减少命令模型(MOR)方法能够产生实时可操作的数字双胞胎,这可以在工业中产生各种新的价值流。传统的预测方法对于线性问题是稳健和准确的,而采用机器学习处理非线性则成为减少复杂问题的一个新选择。这种方法通常由两个步骤组成。第一步是通过投影方法降低尺寸,第二个步骤是神经网络的模型重建。在这项工作中,我们分别对两个步骤进行一些修改,并用三个模拟模型调查它们如何受到测试的影响。在所有案例中,正正正正正正正方形变形(POD)被用于减少尺寸。对于这一步骤,用恒定输入参数生成输入快照数据库的效果与持续输入参数进行比较。对于模型重建步骤,比较了两种神经网络结构类型:多层 Perceptron(MLP)和Runge-Kutta Neural 网络(RKNNN)。MLP直接学习系统状态,而RKNNN在RKNN学习系统外导出并预测新状态为Ringge-Kutta Ingrototor。