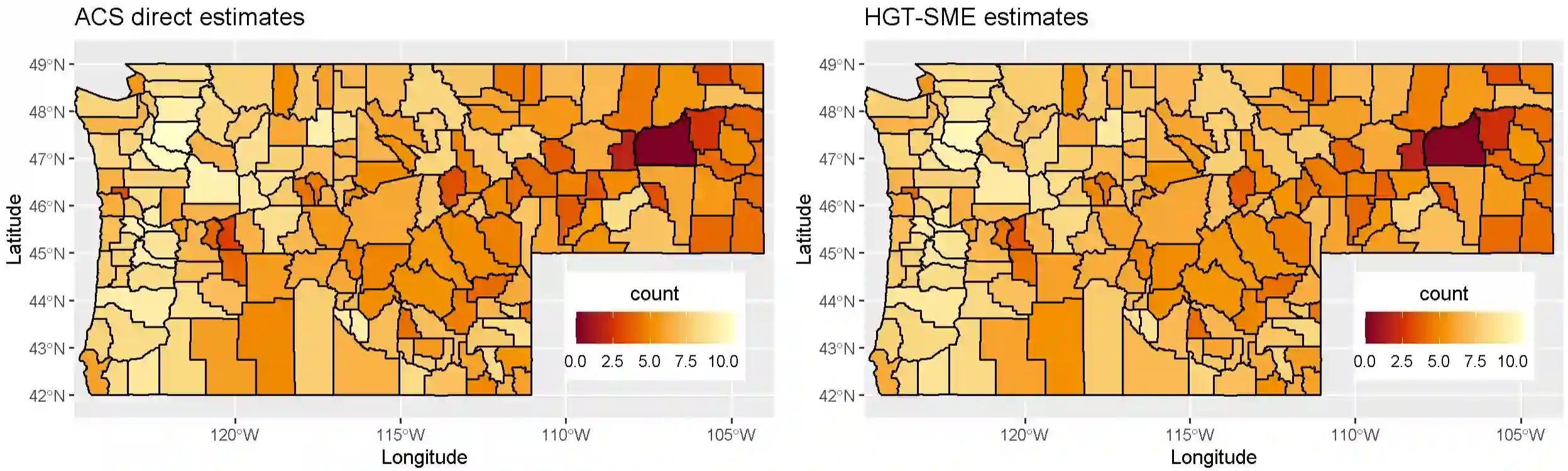
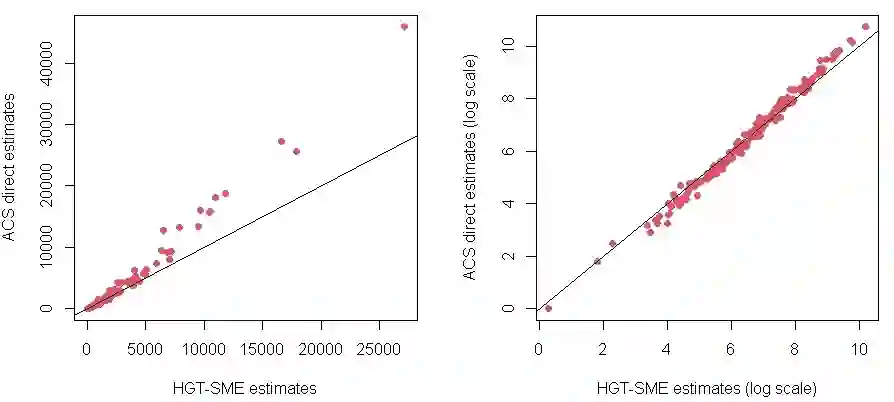
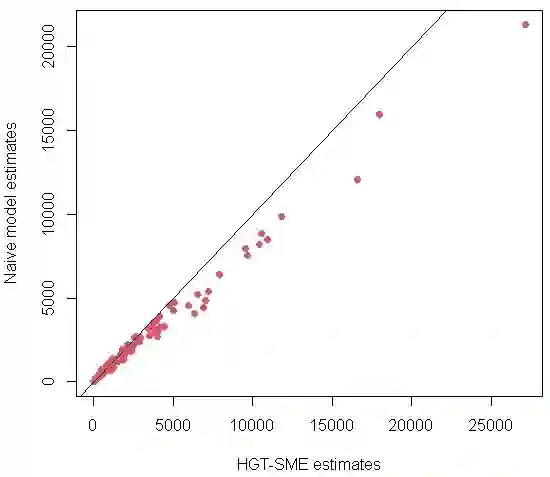
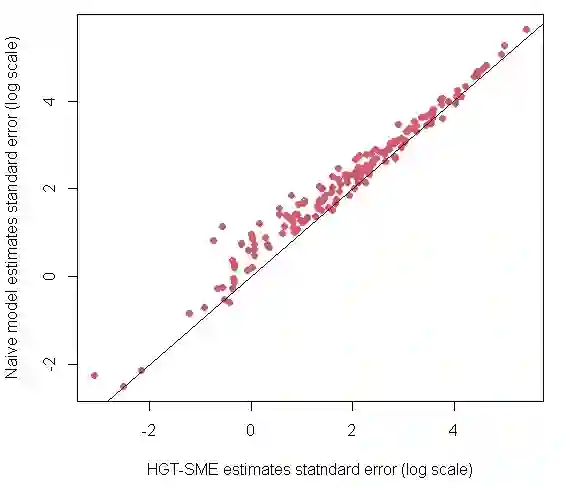
We introduce Bayesian hierarchical models for predicting high-dimensional tabular survey data which can be distributed from one or multiple classes of distributions (e.g., Gaussian, Poisson, Binomial, etc.). We adopt a Bayesian implementation of a Hierarchical Generalized Transformation (HGT) model to deal with the non-conjugacy of non-Gaussian data models when estimated using a Latent Gaussian Process (LGP) model. Survey data are usually prone to a high degree of sampling error, and we use covariates that are prone to measurement error as well as those free of any such error. A classical measurement error component is defined to deal with the sampling error in the covariates. The proposed models can be high-dimensional and we employ the notion of basis function expansions to provide an effective approach to dimension reduction. The HGT component lends flexibility to our model to incorporate multi-type response datasets under a unified latent process model framework. To demonstrate the applicability of our methodology, we provide the results from simulation studies and data applications arising from a dataset consisting of the U.S. Census Bureau's American Community Survey (ACS) 5-year period estimates of the total population count under the poverty threshold and the ACS 5-year period estimates of median housing costs at the county level across multiple states in the USA.
翻译:我们采用巴伊西亚等级模型来预测可以从一个或多个分布类别(例如高森、普瓦松、比诺莫拉尔等)中分布的高层次表调查数据; 我们采用巴伊西亚实施高层次通用变换(HGT)模型,以处理使用低层高叙进程模型估计非加苏西人数据模型不兼容的问题; 调查数据通常容易发生高程度的抽样错误,我们使用易于测量误差和无任何此类误差的变量。 典型的计量误差部分被确定为处理同级差的抽样误差。 拟议的模型可以是高层次的,我们采用基础功能扩展概念,为降低尺寸提供有效办法。 HGT部分为我们的模式提供了灵活性,以在统一的潜在进程模型框架内纳入多类型反应数据集。 为了证明我们的方法的适用性,我们提供了由美国统计局在5年期的美国人口标准值中位估算(美国统计局在5年期的美国人口-美国人口-美国人口-美国人口-美国人口-统计局的统计5年期)中标数据估算中产生的模拟研究和数据应用数据应用结果。