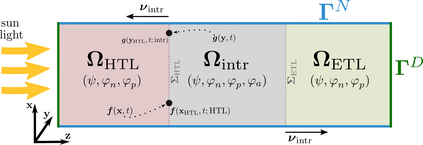
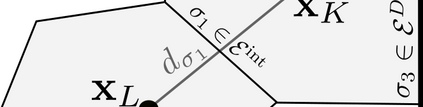
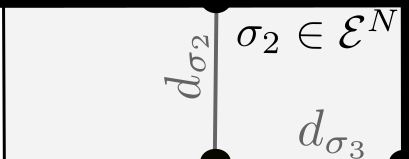
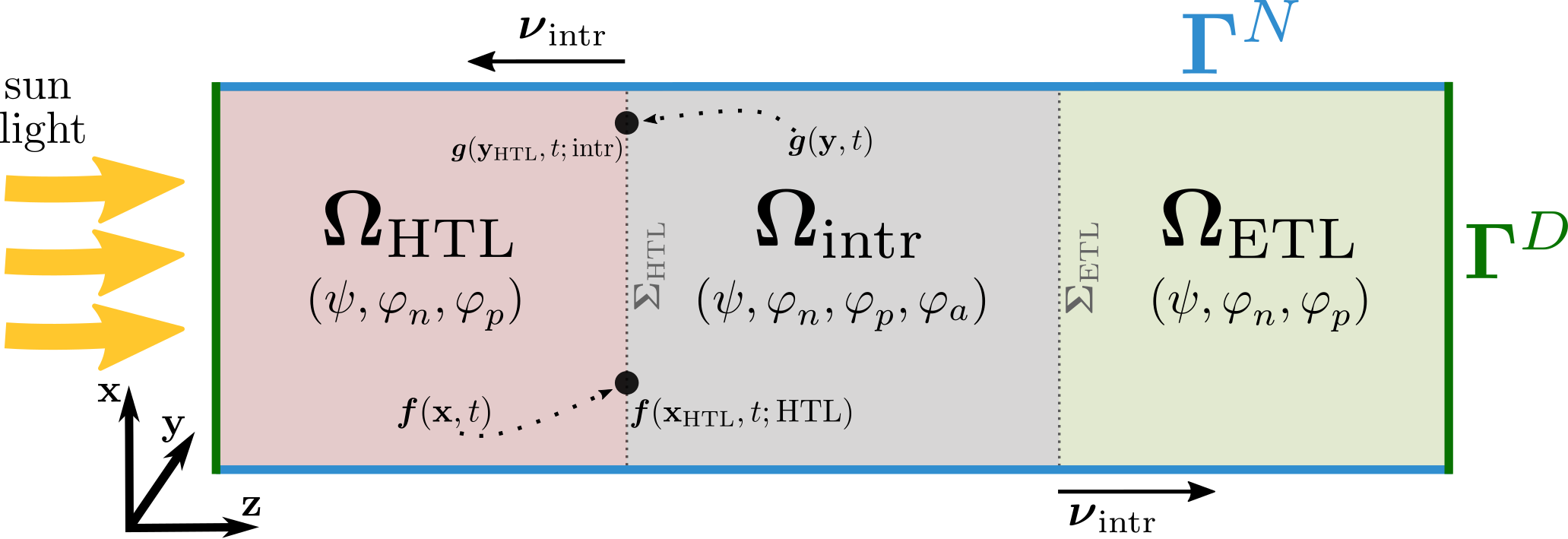
In this paper, we consider a drift-diffusion charge transport model for perovskite solar cells, where electrons and holes may diffuse linearly (Boltzmann approximation) or nonlinearly (e.g. due to Fermi-Dirac statistics). To incorporate volume exclusion effects, we rely on the Fermi-Dirac integral of order -1 when modeling moving anionic vacancies within the perovskite layer which is sandwiched between electron and hole transport layers. After non-dimensionalization, we first prove a continuous entropy-dissipation inequality for the model. Then, we formulate a corresponding two-point flux finite volume scheme on Voronoi meshes and show an analogous discrete entropy-dissipation inequality. This inequality helps us to show the existence of a discrete solution of the nonlinear discrete system with the help of a corollary of Brouwer's fixed point theorem and the minimization of a convex functional. Finally, we verify our theoretically proven properties numerically, simulate a realistic device setup and show exponential decay in time with respect to the L^2 error as well as a physically and analytically meaningful relative entropy.
翻译:在本文中,我们考虑的是百草枯太阳能电池的流散充电传输模型,其中电子和孔洞可以线性地扩散(Boltzmann近似)或非线性地扩散(例如Fermi-Dirac的统计数字)。要纳入排量效应,我们依靠Fermi-Dirac 集序集成 -1 来建模在电子和洞性运输层之间混合的透气层内移动阴离散空缺。在非维化后,我们首先证明该模型具有持续的星盘分解不平等性。然后,我们在Voranoonoi meshes上制定相应的两点通量定量法,并显示类似的离离散的分解分解分解不平等性。这种不平等有助于我们展示非线性离散的系统离解性解决方案的存在,并借助于布鲁韦尔固定点的定点的定点和最小化的矩形功能的必然结果。最后,我们验证了我们经理论上证实的特性,用数字模拟了现实的装置设置,并显示时间指数性衰减,显示与L%2号的相对错误有关的指数。