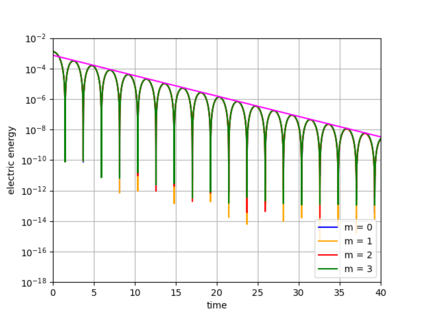
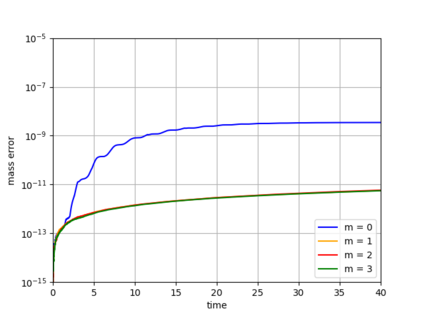
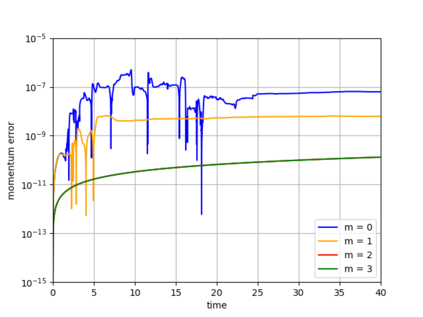
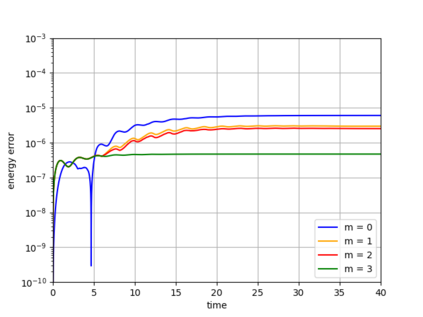
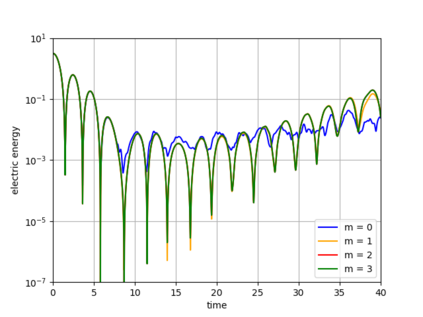
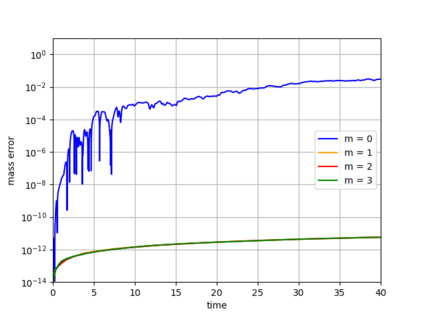
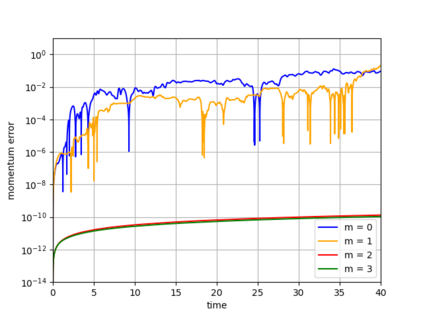
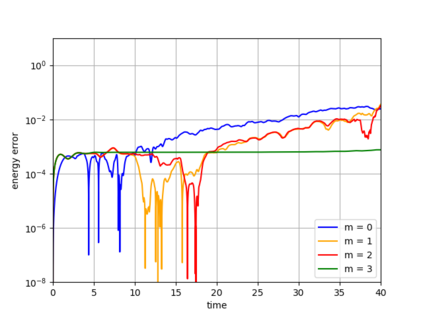
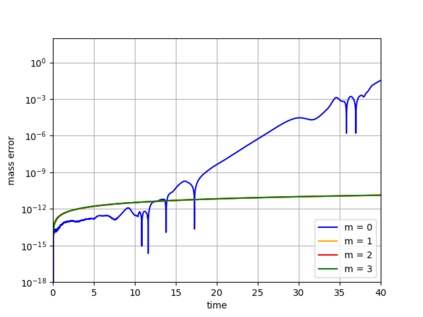
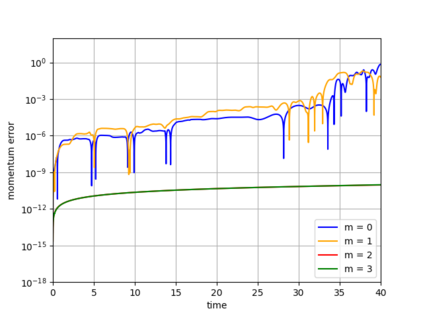
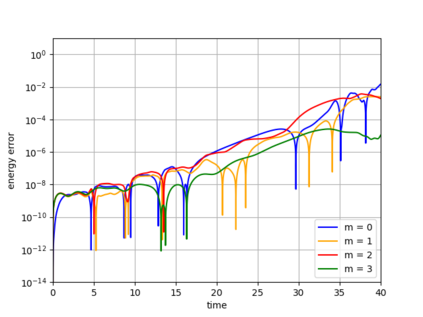
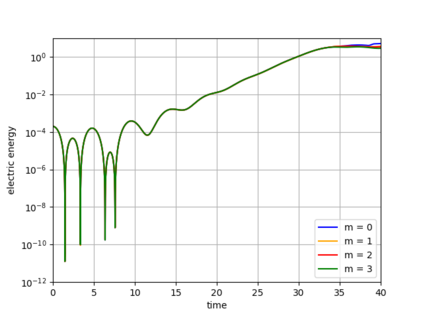
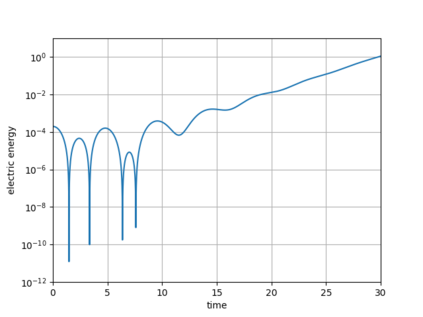
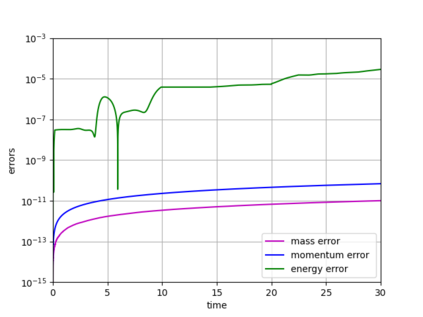
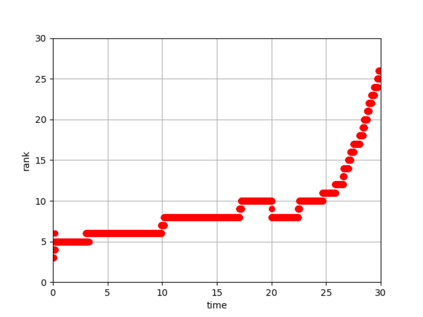
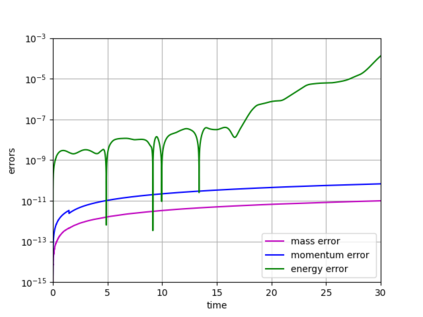
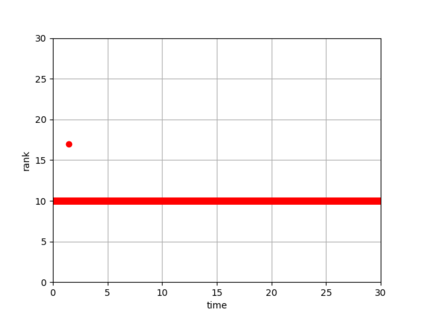
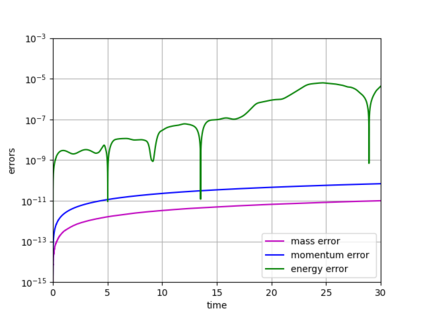
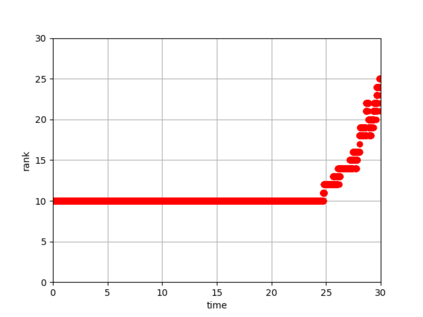
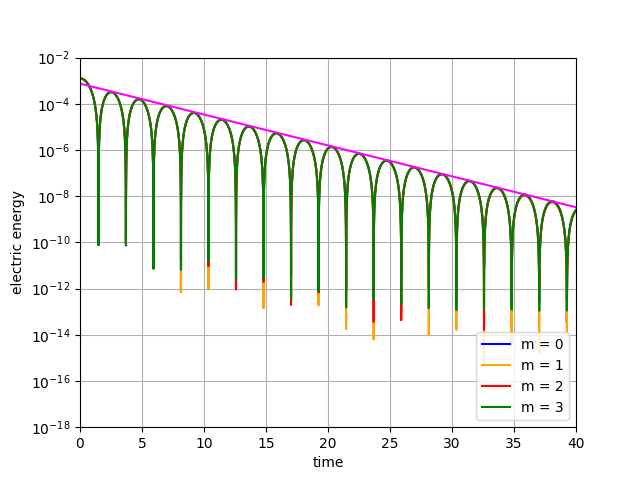
Dynamical low-rank approximation, as has been demonstrated recently, can be extremely efficient in solving kinetic equations. However, a major deficiency is that they do not preserve the structure of the underlying physical problem. For example, the classic dynamical low-rank methods violate mass, momentum, and energy conservation. In [L. Einkemmer, I. Joseph, J. Comput. Phys. 443:110495, 2021] a conservative dynamical low-rank approach has been proposed. However, directly integrating the resulting equations of motion, similar to the classic dynamical low-rank approach, results in an ill-posed scheme. In this work we propose a robust, i.e. well-posed, integrator for the conservative dynamical low-rank approach that conserves mass and momentum (up to machine precision) and significantly improves energy conservation. We also report improved qualitative results for some problems and show how the approach can be combined with a rank adaptive scheme.
翻译:正如最近所显示的,动态低位近似法在解决动能方程方面可能极为有效。然而,一个重大缺陷是它们没有保存基本物理问题的结构。例如,典型的动态低位法侵犯了质量、动力和节能。在[L. Einkemmer, I. Joseph, J. Comput, Phys. 443:110495, 2021] 中,提出了保守的动态低位法。然而,直接结合由此产生的运动方程,类似于典型的动态低位法,导致了一个错误的计划。在这项工作中,我们提出了一个稳健的、即完善的、集成的保守的动态低位法,以保持质量和动力(达到机器精确程度),并大大改善节能。我们还报告了一些问题的质量结果,并表明该方法如何与等级适应计划相结合。