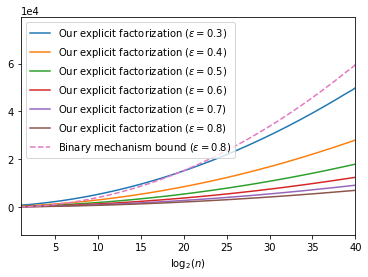
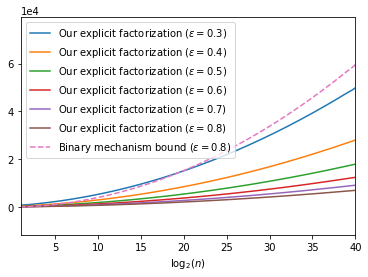
The first large-scale deployment of private federated learning uses differentially private counting in the continual release model as a subroutine (Google AI blog titled "Federated Learning with Formal Differential Privacy Guarantees"). In this case, a concrete bound on the error is very relevant to reduce the privacy parameter. The standard mechanism for continual counting is the binary mechanism. We present a novel mechanism and show that its mean squared error is both asymptotically optimal and a factor 10 smaller than the error of the binary mechanism. We also show that the constants in our analysis are almost tight by giving non-asymptotic lower and upper bounds that differ only in the constants of lower-order terms. Our algorithm is a matrix mechanism for the counting matrix and takes constant time per release. We also use our explicit factorization of the counting matrix to give an upper bound on the excess risk of the private learning algorithm of Denisov et al. (NeurIPS 2022). Our lower bound for any continual counting mechanism is the first tight lower bound on continual counting under approximate differential privacy. It is achieved using a new lower bound on a certain factorization norm, denoted by $\gamma_F(\cdot)$, in terms of the singular values of the matrix. In particular, we show that for any complex matrix, $A \in \mathbb{C}^{m \times n}$, \[ \gamma_F(A) \geq \frac{1}{\sqrt{m}}\|A\|_1, \] where $\|\cdot \|$ denotes the Schatten-1 norm. We believe this technique will be useful in proving lower bounds for a larger class of linear queries. To illustrate the power of this technique, we show the first lower bound on the mean squared error for answering parity queries.
翻译:在连续发布模式中,首次大规模部署私人联邦学习 {的大规模部署 { 使用不同的私人计数作为子例程( Google AI 博客名为“ 正式差异隐私保障的联邦学习 ” ) 。 在这种情况下, 错误的混凝土绑定对于减少隐私参数非常相关。 连续计算的标准机制是二进制机制。 我们提出了一个新机制, 显示其平均正方差既不具有试想性, 也比二进制机制差差10。 我们还显示, 我们分析中的常数几乎是紧紧的, 因为它给出了非默认值的下限, 只在更低顺序的常数中提供不同的非默认值下限 。 我们的算法是一个矩阵矩阵矩阵的矩阵化矩阵机制, 显示一个新的直线性值 。
相关内容
Source: Apple - iOS 8