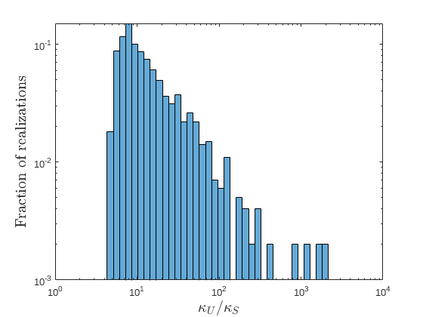
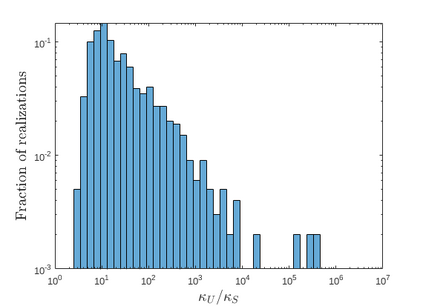
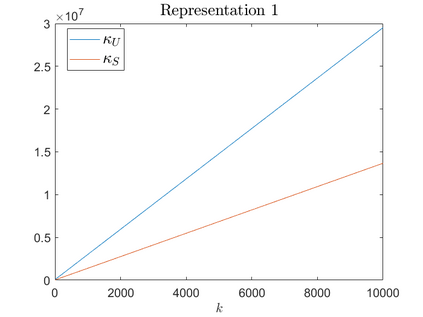
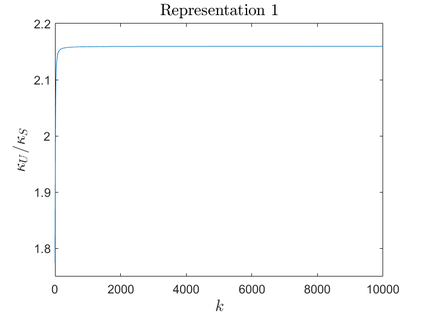
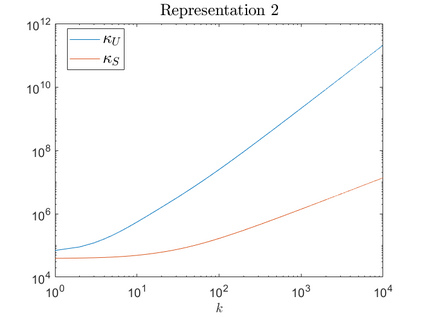
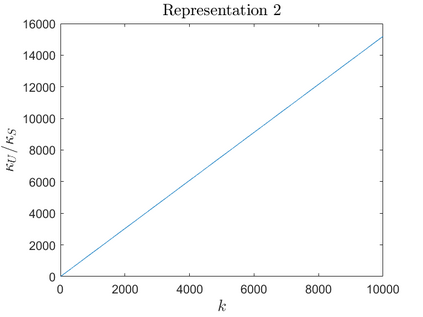
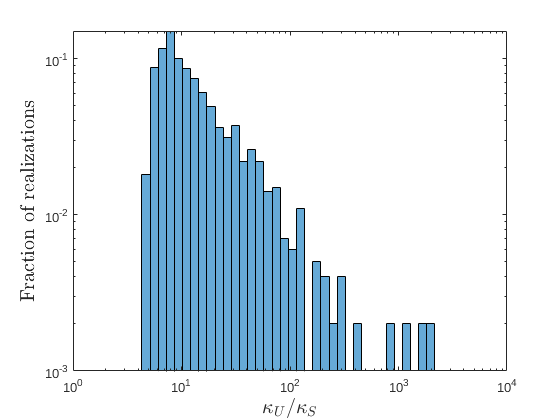
Zeros of rational transfer function matrices $R(\lambda)$ are the eigenvalues of associated polynomial system matrices $P(\lambda)$, under minimality conditions. In this paper we define a structured condition number for a simple eigenvalue $\lambda_0$ of a (locally) minimal polynomial system matrix $P(\lambda)$, which in turn is a simple zero $\lambda_0$ of its transfer function matrix $R(\lambda)$. Since any rational matrix can be written as the transfer function of a polynomial system matrix, our analysis yield a structured perturbation theory for simple zeros of rational matrices $R(\lambda)$. To capture all the zeros of $R(\lambda)$, regardless of whether they are poles or not, we consider the notion of root vectors. As corollaries of the main results, we pay particular attention to the special case of $\lambda_0$ being not a pole of $R(\lambda)$ since in this case the results get simpler and can be useful in practice. We also compare our structured condition number with Tisseur's unstructured condition number for eigenvalues of matrix polynomials, and show that the latter can be unboundedly larger. Finally, we corroborate our analysis by numerical experiments.
翻译:合理转移函数矩阵的零值 $R (\ lambda) $R (\ lambda) 是相关多元系统矩阵在最低条件条件下的外值 $P (\ lambda) 。 在本文中, 我们定义了一个简单的( 本地) 最小多元系统矩阵的结构性条件值$\ lambda_ 0美元( 本地) $P (\ lambda) $( lambda) $( lambda) $ (美元) 。 由于任何合理的矩阵可以写成一个多边系统矩阵的转移函数 $P (\ lambda) $( lambda) $( lambda) $( 当地) 最低( 当地) 最低多元系统矩阵矩阵 $( $ ( lambda) $ ( lambda) $ ( ) $ ( 当地) 0. 0 $( 当地) ) 最低组合系统矩阵 $ ( $ ( ) $ ( lambbda) $ ( lambda) ) ) $ ( 0) $ ( 0) $ ( ) 美元) 美元 ( 美元) 美元 美元 美元 美元 美元) 美元 ( 美元) 美元) 美元 ( 美元) 美元) 美元 ( 美元) 美元) 美元( 美元) 美元) 美元( 美元) 美元) 美元( 美元) 美元( 美元) 美元) 美元( 美元) 美元) 美元( 美元) 美元( 美元) 美元) 美元( 美元) 美元( 美元) 美元) 美元( 美元) 美元( 美元) 美元) ) ) 美元( 美元) 美元( 美元( 美元) 美元) 美元) 美元( 美元) 美元) 美元) 美元( 美元) 美元) 美元( 美元) 美元( 美元) 美元( 美元) 美元) 美元) 美元) 美元) 美元) 美元) 美元( 美元( 美元) 美元) 美元) 美元) 美元) 美元) 美元(