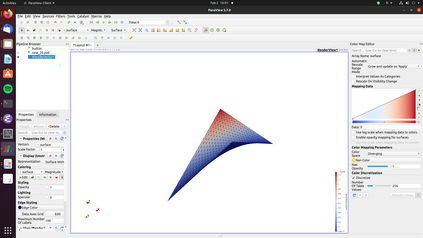
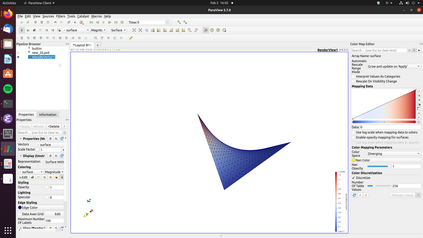
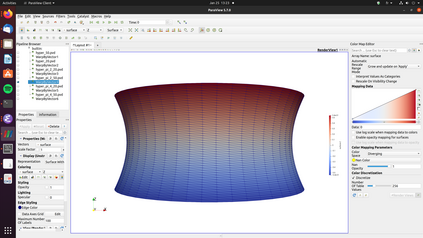
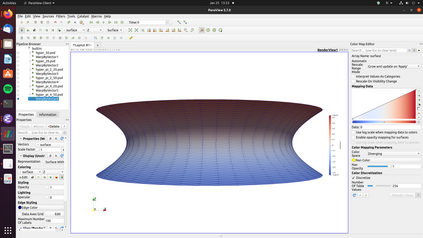
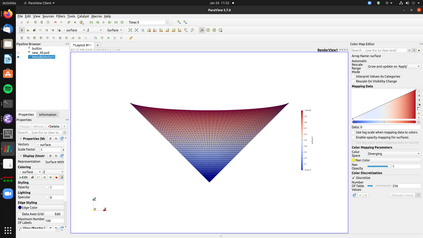
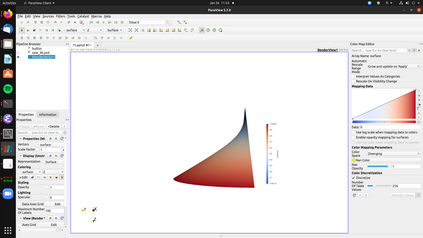
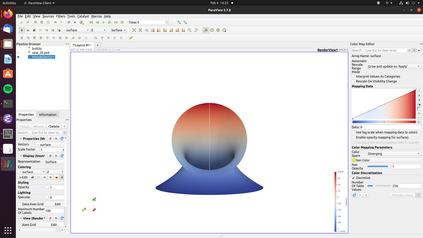
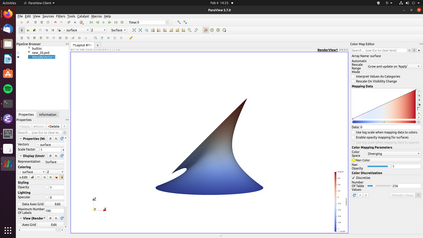
A nonlinear partial differential equation (PDE) that models the possible shapes that a periodic Miura tessellation can take in the homogenization limit has been established recently and solved only in specific cases. In this paper, the existence and uniqueness of a solution to the PDE is proved for general Dirichlet boundary conditions. Then a H^2-conforming discretization is introduced to approximate the solution of the PDE and a fixed point algorithm is proposed to solve the associated discrete problem. A convergence proof for the method is given as well as a convergence rate. Finally, numerical experiments show the robustness of the method and that non trivial shapes can be achieved using periodic Miura tessellations.
翻译:一种非线性部分差异方程式(PDE),该方程式模型模拟了Miura周期间断熔化在同质化极限中可能呈现的形状,最近才确定了这种形状,只有在具体情况下才予以解决;在本文中,对于一般的Drichlet边界条件,PDE解决方案的存在和独特性得到了证明;然后引入了一种与PDE解决方案相匹配的分解法,以近似相关离散问题的解决方案,并提出了一个固定点算法,以解决相关的离散问题。提供了该方法的趋同证据以及一个趋同率。最后,数字实验显示了该方法的稳健性,以及使用定期的 Miura 熔融化法可以实现的非微小形状。