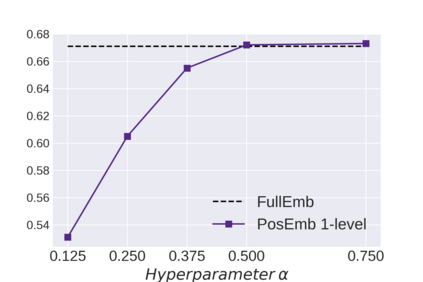
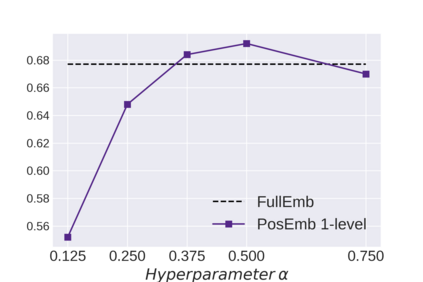
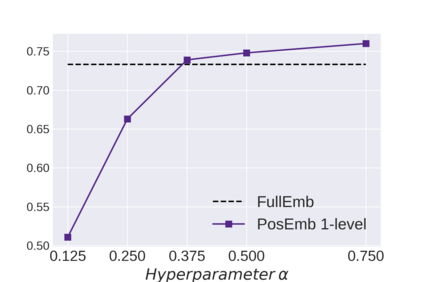
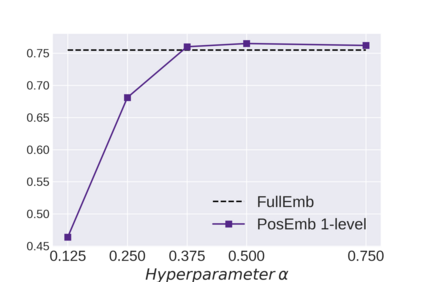
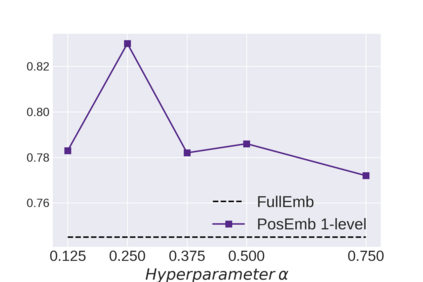
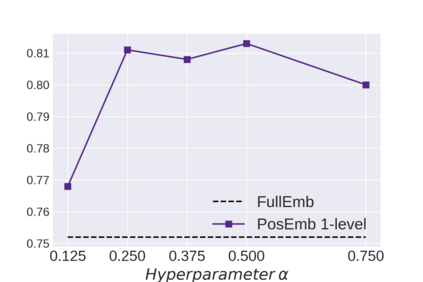
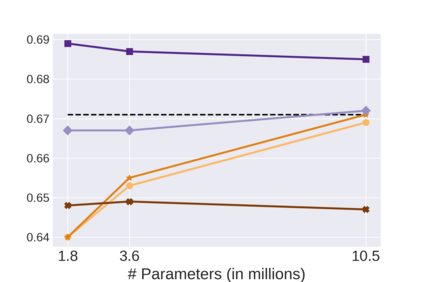
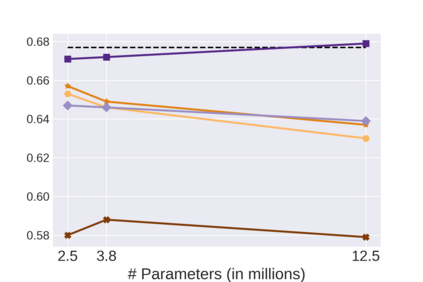
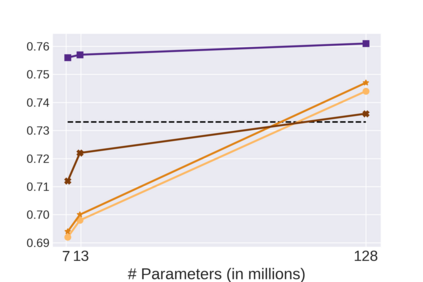
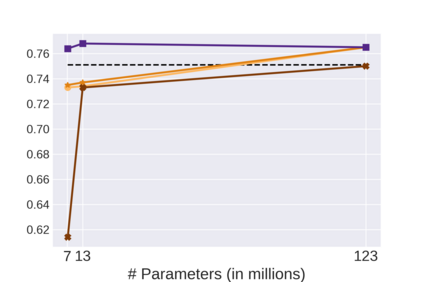
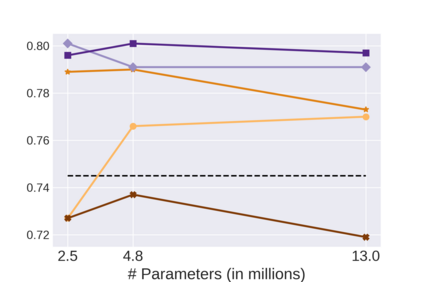
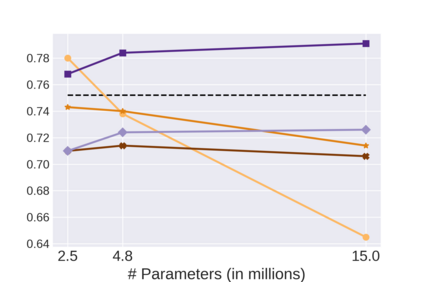
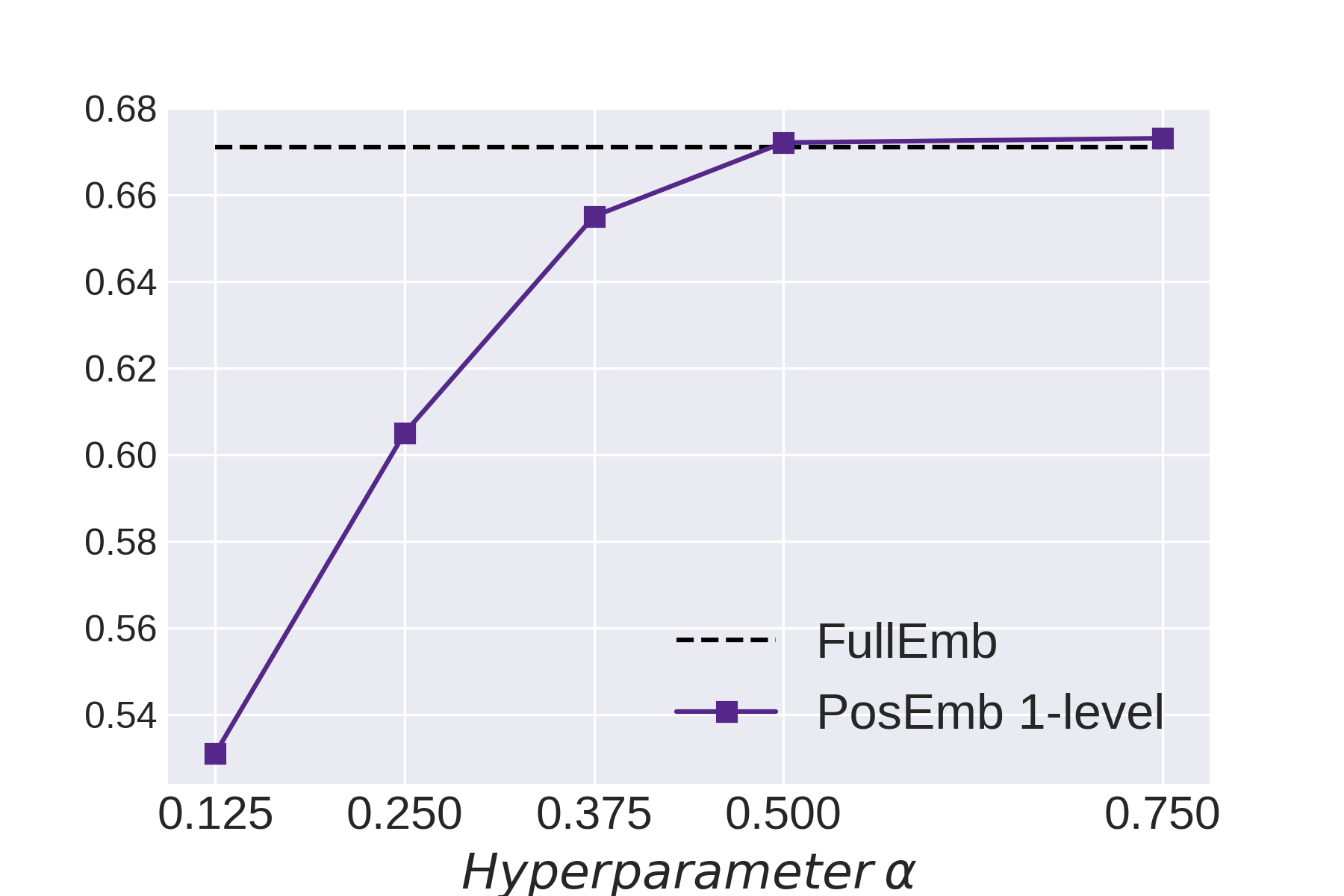
Graph Neural Networks (GNNs) bring the power of deep representation learning to graph and relational data and achieve state-of-the-art performance in many applications. GNNs compute node representations by taking into account the topology of the node's ego-network and the features of the ego-network's nodes. When the nodes do not have high-quality features, GNNs learn an embedding layer to compute node embeddings and use them as input features. However, the size of the embedding layer is linear to the product of the number of nodes in the graph and the dimensionality of the embedding and does not scale to big data and graphs with hundreds of millions of nodes. To reduce the memory associated with this embedding layer, hashing-based approaches, commonly used in applications like NLP and recommender systems, can potentially be used. However, a direct application of these ideas fails to exploit the fact that in many real-world graphs, nodes that are topologically close will tend to be related to each other (homophily) and as such their representations will be similar. In this work, we present approaches that take advantage of the nodes' position in the graph to dramatically reduce the memory required, with minimal if any degradation in the quality of the resulting GNN model. Our approaches decompose a node's embedding into two components: a position-specific component and a node-specific component. The position-specific component models homophily and the node-specific component models the node-to-node variation. Extensive experiments using different datasets and GNN models show that our methods are able to reduce the memory requirements by 88% to 97% while achieving, in nearly all cases, better classification accuracy than other competing approaches, including the full embeddings.
翻译:内建网络( GNNS) 带来深层代表学习用于图形和关系数据的力量, 并在许多应用程序中实现最先进的性能。 GNNS 计算节点表示方式时, 要考虑到节点的自我网络的表层学和自我网络节点的特征。 当节点没有高质量特性时, GNNS 学习嵌入层以计算节点嵌入并用作输入特性。 然而, 嵌入层的大小是直线到图形节点数的产物, 嵌入的维度不高。 GNNNNS 计算节点表示方式时, 计算节点表示方式时, 将考虑到节点的表层的表层, 而不是以数亿个节点的节点表示方式计算。 直接应用这些思想时, 无法利用许多真实世界的图表中的所有节点, 表面上接近的节点往往与图表中的节点位置相关, 嵌入的尺寸不直径直方位和直径直径的直方表示方式, 将让我们的内建的直方位和直方位更接近于正态的直方位, 直方位表示方式显示的直方位的直方位的直方位将显示, 。 直方位将显示的平方位方法将显示的平方位的直方位将显示为直方位将显示为直方位。