Feature Enforcing PINN (FE-PINN): A Framework for Learning the Underlying-Physics to Resolve Unbalancing in the Objective Function Terms

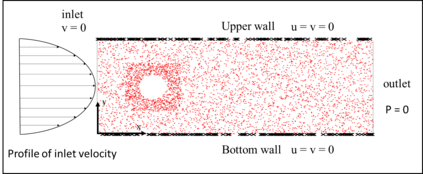
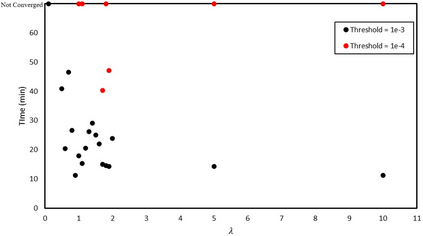
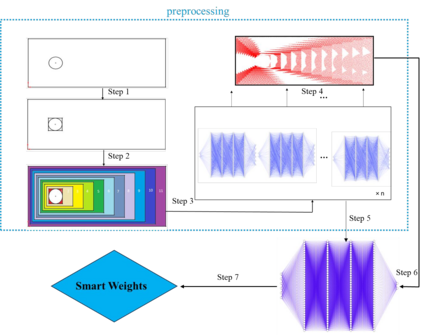
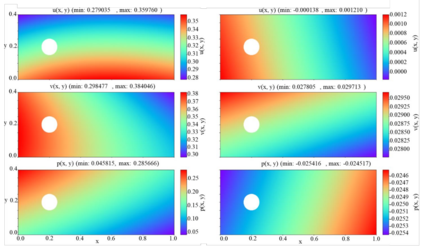
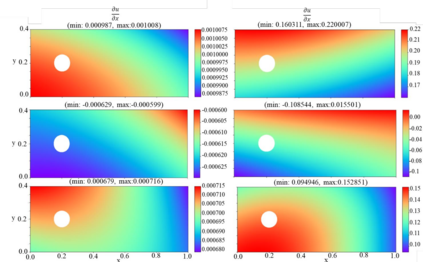
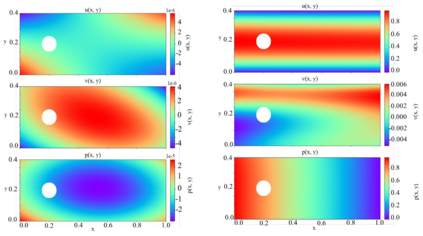
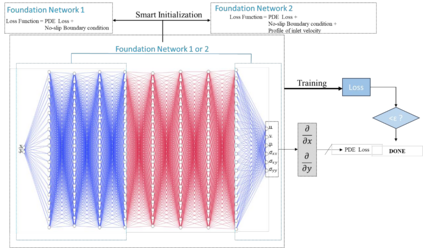
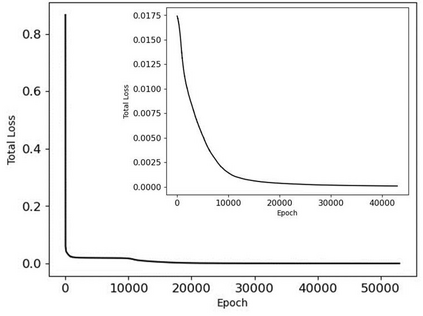
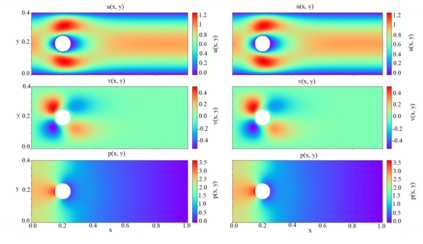
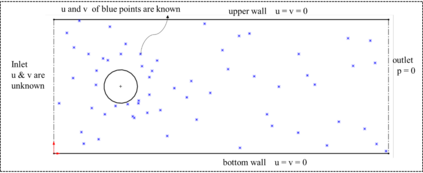
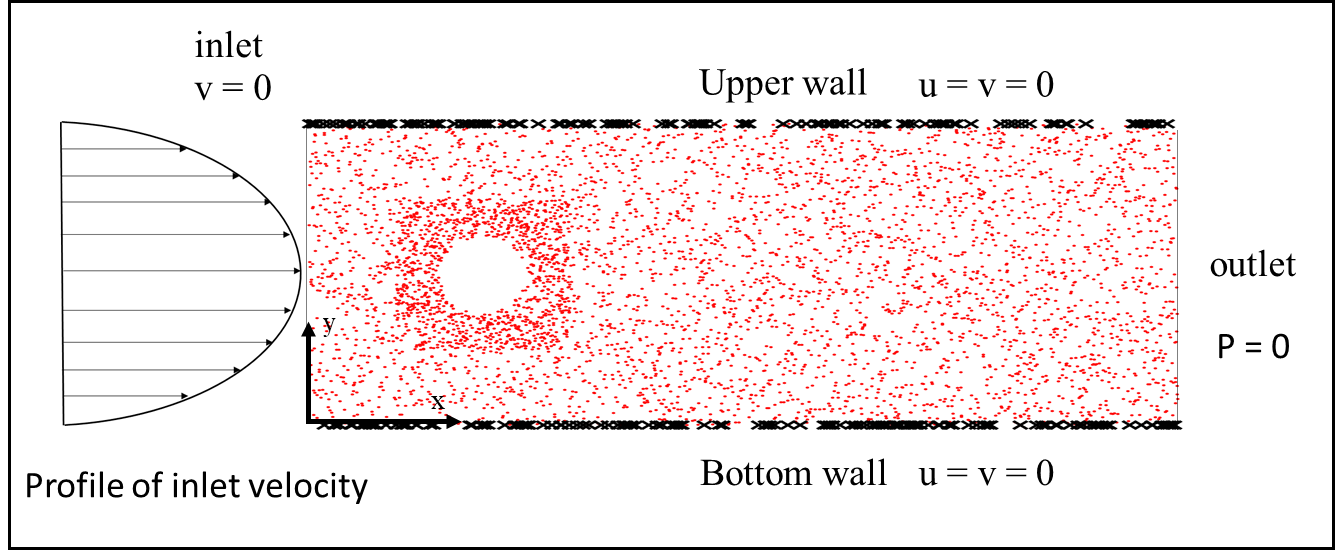
In this study, we propose a new data-free framework, Feature Enforcing Physics Informed Neural Network (FE-PINN), to overcome the challenge of an imbalanced loss function in vanilla PINNs. The imbalance is caused by the presence of two terms in the loss function: the partial differential loss and the boundary condition mean squared error. A standard solution is to use loss weighting, but it requires hyperparameter tuning. To address this challenge, we introduce a process called smart initialization to force the neural network to learn only the boundary conditions before the final training in a designed process. In this method, clustered domain points are used to train a neural network with designed weights, resulting in the creation of a neural network called Foundation network. This results in a network with unique weights that understand boundary conditions. Then, additional layers are used to improve the accuracy. This solves the problem of an imbalanced loss function without further need for hyperparameter tuning. For 2D flow over a cylinder as a benchmark, smart initialization in FE-PINN is 574 times faster than hyperparameter tuning in vanilla PINN. Even with the optimal loss weight value, FE-PINN outperforms vanilla PINN by speeding up the average training time by 1.98. Also, the ability of the proposed approach is shown for an inverse problem. To find the inlet velocity for a 2D flow over a cylinder, FE-PINN is twice faster than vanilla PINN with the knowledge of optimal weight loss value for vanilla PINN. Our results show that FE-PINN not only eliminates the time-consuming process of loss weighting but also improves convergence speed compared to vanilla PINN, even when the optimal weight value is used in its loss function. In conclusion, this framework can be used as a fast and accurate tool for solving a wide range of Partial Differential Equations across various fields.