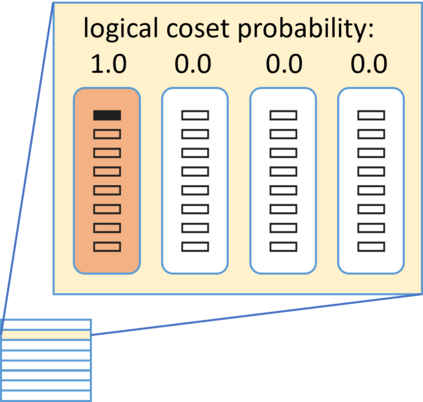
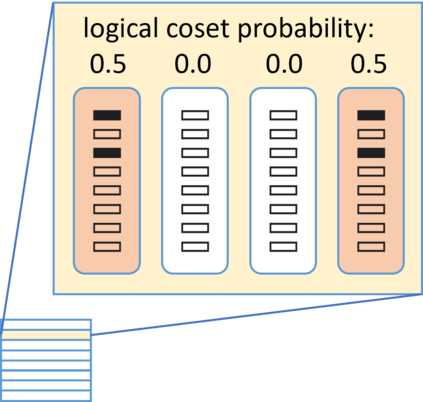
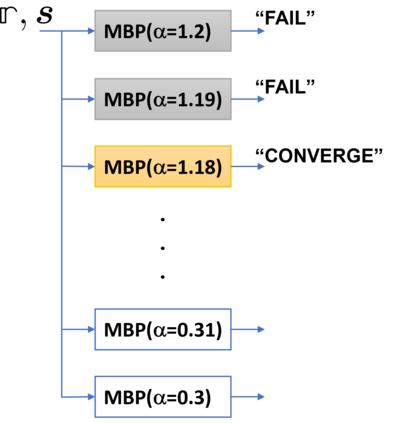
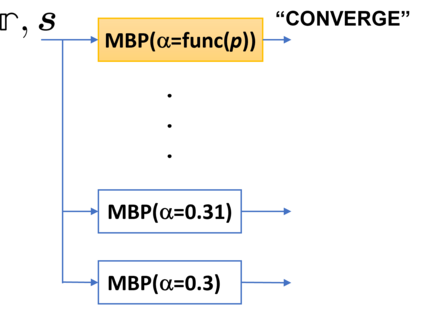
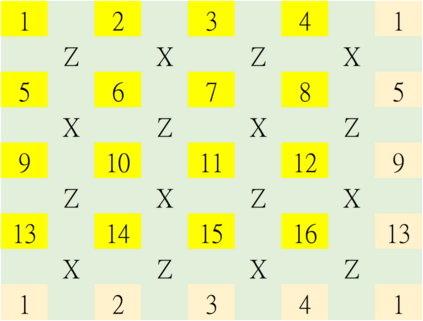
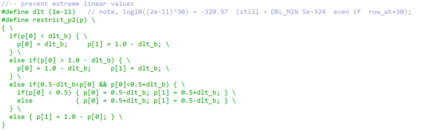
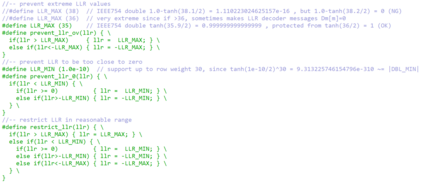
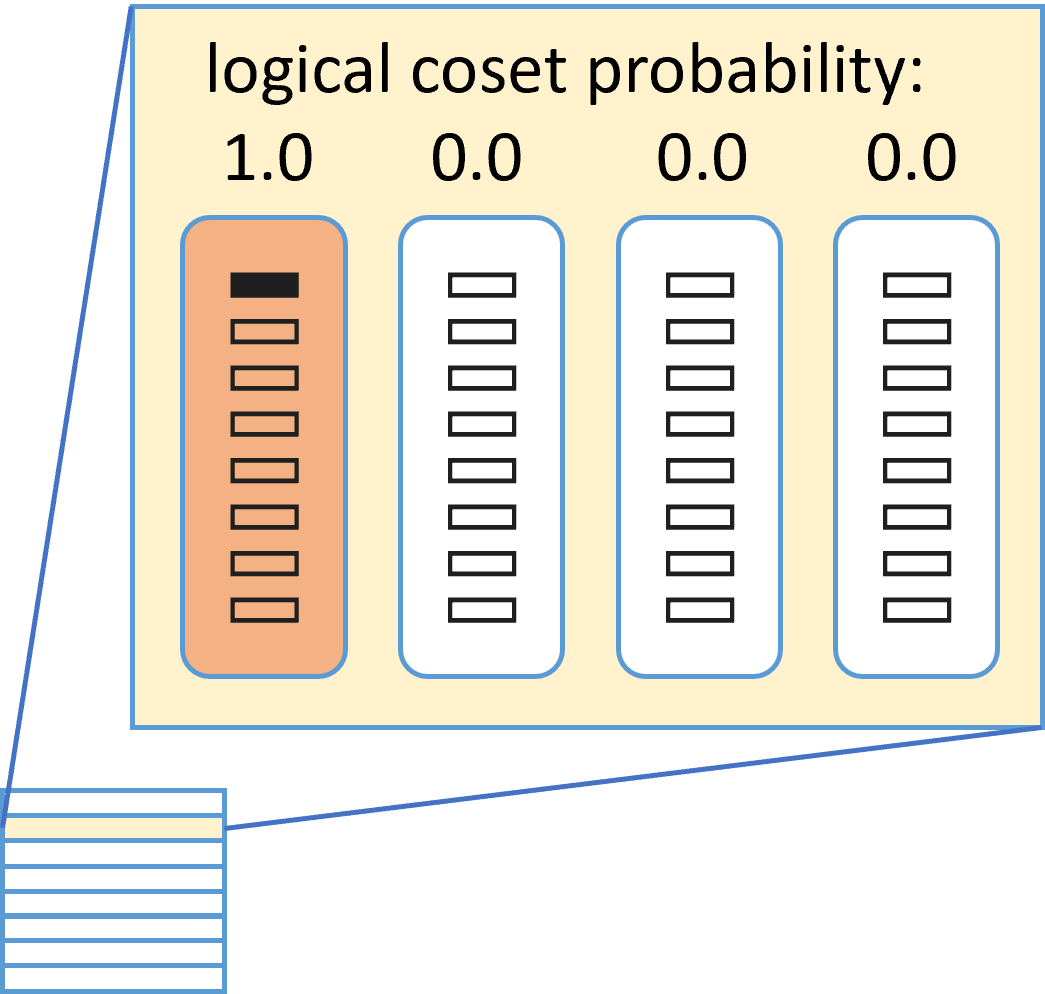
Erasures are the primary type of errors in physical systems dominated by leakage errors. While quantum error correction (QEC) using stabilizer codes can combat these error, the question of achieving near-capacity performance with explicit codes and efficient decoders remains a challenge. Quantum decoding is a classical computational problem that decides what the recovery operation should be based on the measured syndromes. For QEC, using an accurate decoder with the shortest possible runtime will minimize the degradation of quantum information while awaiting the decoder's decision. We examine the quantum erasure decoding problem for general stabilizer codes and present decoders that not only run in linear-time but are also accurate. We achieve this by exploiting the symmetry of degenerate errors. Numerical evaluations show near maximum-likelihood decoding for various codes, achieving capacity performance with topological codes and near-capacity performance with non-topological codes. We furthermore explore the potential of our decoders to handle other error models, such as mixed erasure and depolarizing errors, and also local deletion errors via concatenation with permutation invariant codes.
翻译:暂无翻译