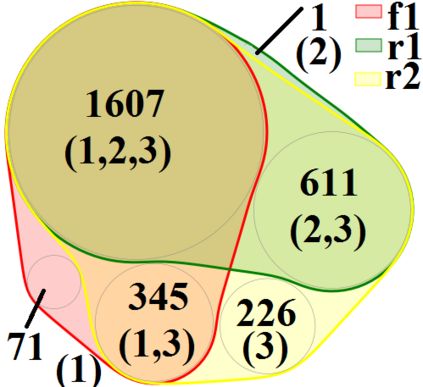
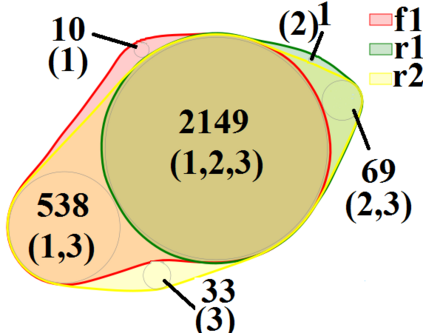
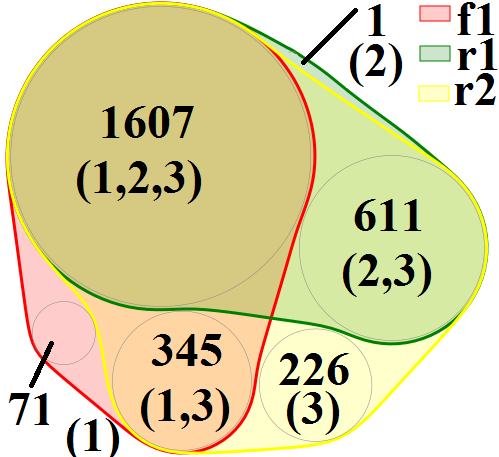
Non-negative Matrix Factorization (NMF) is an intensively used technique for obtaining parts-based, lower dimensional and non-negative representation of non-negative data. It is a popular method in different research fields. Scientists performing research in the fields of biology, medicine and pharmacy often prefer NMF over other dimensionality reduction approaches (such as PCA) because the non-negativity of the approach naturally fits the characteristics of the domain problem and its result is easier to analyze and understand. Despite these advantages, it still can be hard to get exact characterization and interpretation of the NMF's resulting latent factors due to their numerical nature. On the other hand, rule-based approaches are often considered more interpretable but lack the parts-based interpretation. In this work, we present a version of the NMF approach that merges rule-based descriptions with advantages of part-based representation offered by the NMF approach. Given the numerical input data with non-negative entries and a set of rules with high entity coverage, the approach creates the lower-dimensional non-negative representation of the input data in such a way that its factors are described by the appropriate subset of the input rules. In addition to revealing important attributes for latent factors, it allows analyzing relations between these attributes and provides the exact numerical intervals or categorical values they take. The proposed approach provides numerous advantages in tasks such as focused embedding or performing supervised multi-label NMF.
翻译:在生物学、医学和药用领域进行研究的科学家往往更倾向于NMF而不是其他减少维度方法(如五氯苯甲醚),因为这种方法的非增强性自然符合域问题的特点,其结果更易于分析和理解。尽管有这些优势,但由于数字性质,很难确切地描述和解释NMF产生的潜在因素。另一方面,基于规则的方法往往被认为更易解释,但缺乏基于部分的解释。在这项工作中,我们提出了一个NMF方法的版本,将基于规则的描述与基于部分的代表性的好处结合起来。鉴于数字输入数据与非否定性的条目以及一套具有高实体覆盖面的规则,该方法仍可能难以准确描述和解释NMFF因其数字性质而导致的潜在因素。 以规则为基础的方法往往被认为更便于解释,但缺乏基于部分的解释。