Manifold GCN: Diffusion-based Convolutional Neural Network for Manifold-valued Graphs

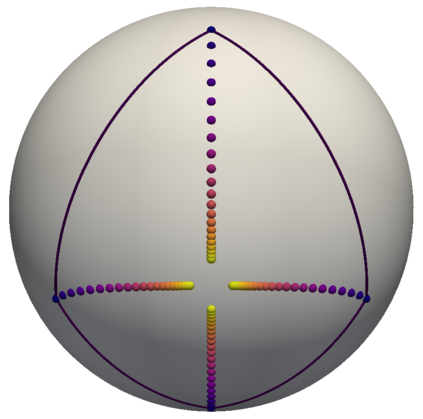
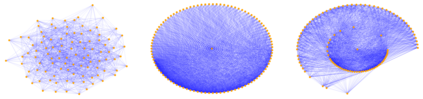
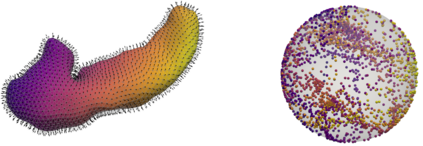
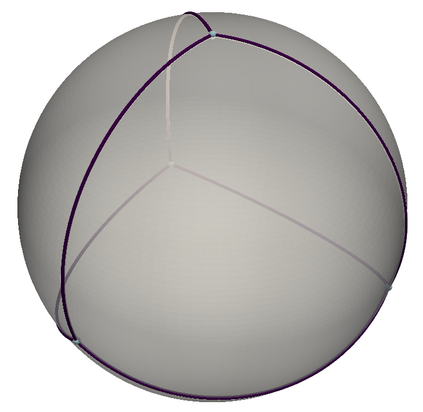
We propose two graph neural network layers for graphs with features in a Riemannian manifold. First, based on a manifold-valued graph diffusion equation, we construct a diffusion layer that can be applied to an arbitrary number of nodes and graph connectivity patterns. Second, we model a tangent multilayer perceptron by transferring ideas from the vector neuron framework to our general setting. Both layers are equivariant with respect to node permutations and isometries of the feature manifold. These properties have been shown to lead to a beneficial inductive bias in many deep learning tasks. Numerical examples on synthetic data as well as on triangle meshes of the right hippocampus to classify Alzheimer's disease demonstrate the very good performance of our layers.