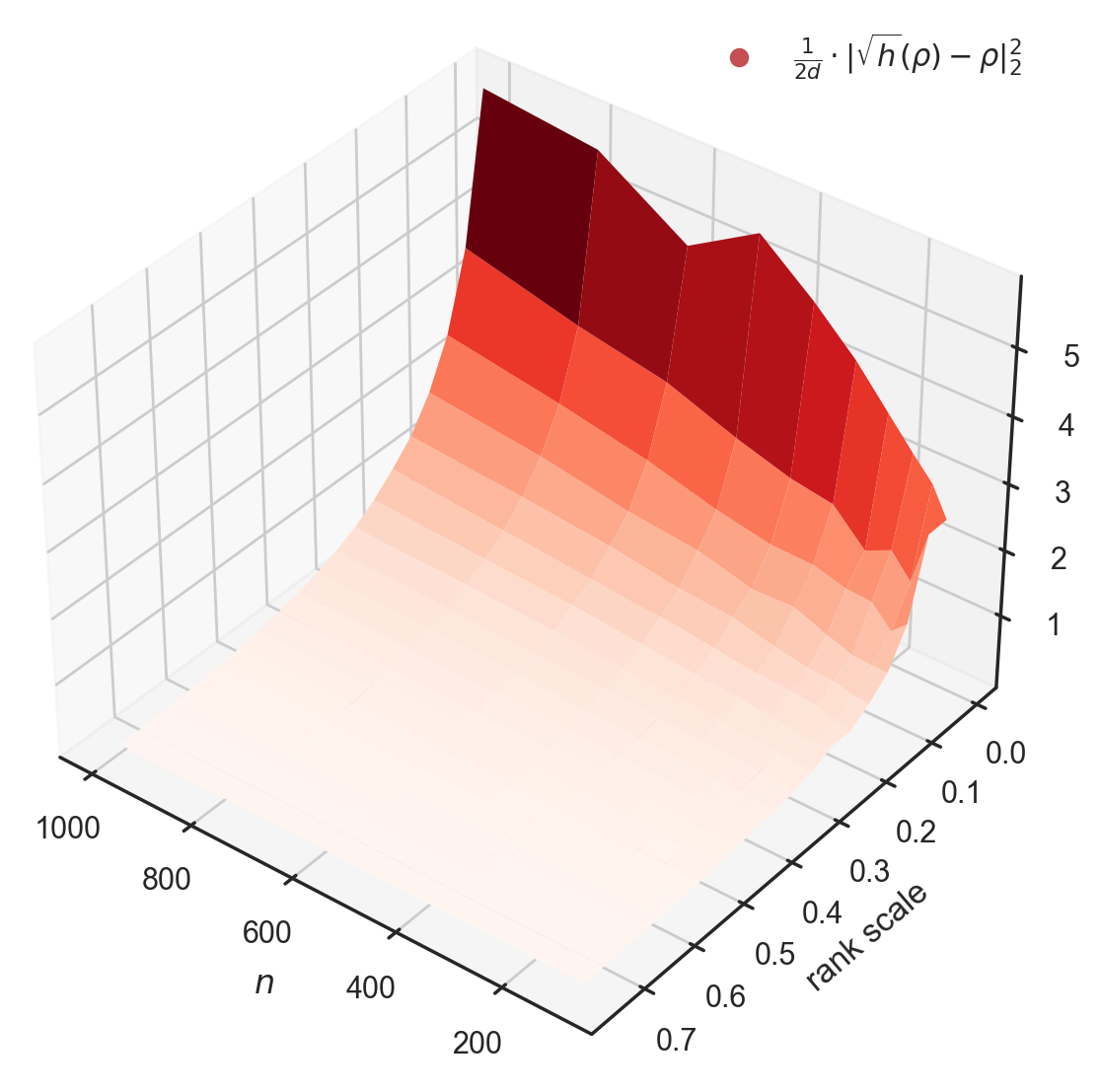
We study algorithms for learning low-rank neural networks -- networks where the weight parameters are re-parameterized by products of two low-rank matrices. First, we present a provably efficient algorithm which learns an optimal low-rank approximation to a single-hidden-layer ReLU network up to additive error $\epsilon$ with probability $\ge 1 - \delta$, given access to noiseless samples with Gaussian marginals in polynomial time and samples. Thus, we provide the first example of an algorithm which can efficiently learn a neural network up to additive error without assuming the ground truth is realizable. To solve this problem, we introduce an efficient SVD-based $\textit{Nonlinear Kernel Projection}$ algorithm for solving a nonlinear low-rank approximation problem over Gaussian space. Inspired by the efficiency of our algorithm, we propose a novel low-rank initialization framework for training low-rank $\textit{deep}$ networks, and prove that for ReLU networks, the gap between our method and existing schemes widens as the desired rank of the approximating weights decreases, or as the dimension of the inputs increases (the latter point holds when network width is superlinear in dimension). Finally, we validate our theory by training ResNet and EfficientNet models on ImageNet.
翻译:我们研究的是学习低级神经网络的算法 -- -- 重量参数由两个低级矩阵产品重新校准的网络。 首先,我们展示了一种可以想象的高效算法,这种算法可以将最优的低级近似值学习到单级低级ReLU网络上,直至添加性差错 $\ epsilon$, 概率为$\ge 1 -\ delta$, 获得无噪音样本,在多元时间和样本中使用高斯边际的无噪音样本。 因此,我们提出了一个新颖的低级初始化框架,用于培训低级 $\ textit{ Netdeept} 网络, 并证明对于RELU网络来说,我们的方法和现有计划之间的缺口是可实现的。为了解决这个问题,我们引入了一种高效的SVD- $\ textitleit{ Nonline cernal Projectionion $$$tal ral ral ral ral ral ral ral ral ral ral ral ral, as the suppreck the supplegal suppral strislation the sluplation subild the slations luplupluplupluplupluplupluplations the slationalitalitalital subild), subild lauttal subild the luptalitalitalitaliztal the the the the the lupal subal subild subal subal subild subild subal subal subal subal subal subaltial subal subal suballine subaltialtialtial subal subal subal subal subal subal subal lax laisl subal lax, subal subal lax, 我们 lax lax, 我们 lax